参考资料

符号动力学是数学中研究符号动力系统的学科。在符号动力系统中，系统的状态可以表示成有限个抽象符号的无穷序列。每个抽象符号都对应一个系统状态，并且系统状态演化的动力学方程，由移位算子（shift operator）对抽象符号序列的作用而给出。由任一状态点的运动轨迹可以通过简单的移位规则来确定。许多复杂动态系统都可以经过变换等价于这类系统，从而可以通过对比较简单的符号动力系统的分析来研究一般动力系统的行为。

数学上，符号动力学的状态通常用符号序列来表示，例如，如果系统有n个状态，可以用n个符号来表示，状态的演变则通过移位算子来描述。例如，一个状态序列可以表示为 ( {s_1, s_2, s_3, ...} )，其中每个 ( s_i ) 是一个符号，代表系统在特定时间点的状态。移位算子 ( \sigma ) 作用于这个序列，产生一个新的序列 ( {s_2, s_3, s_4, ...} )，表示系统状态随时间的演变。

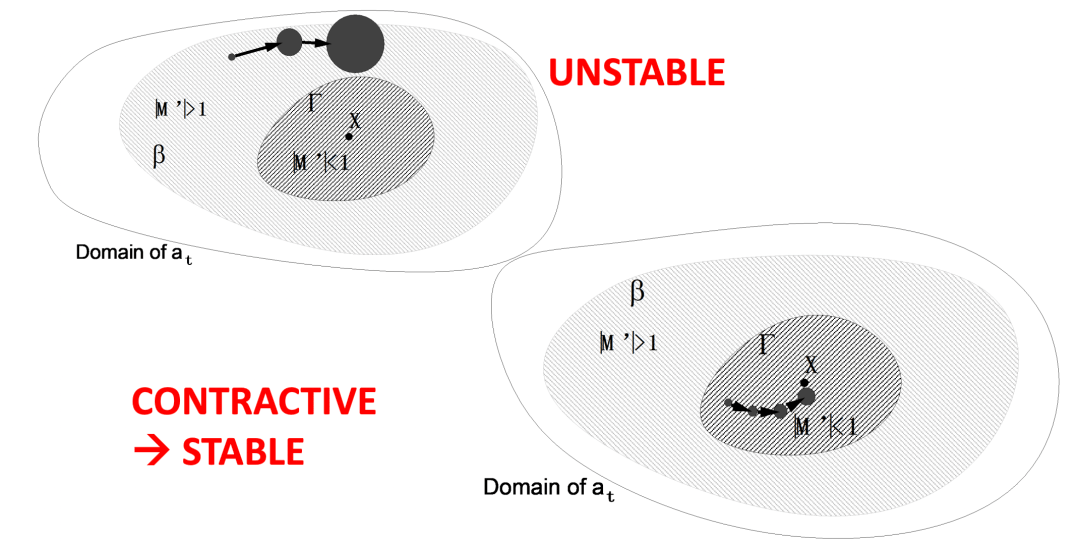
图1：符号动力学示意图

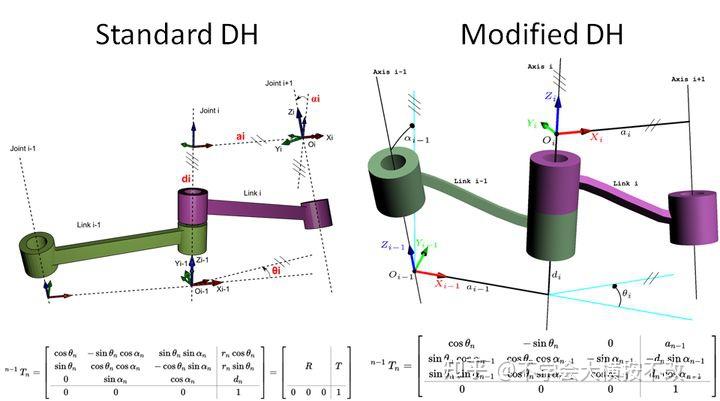
图2：符号动力学状态转移图

这些概念在数学、物理学、生物学等多个领域都有广泛的应用，帮助研究者分析和理解复杂系统的动态行为。