请简要介绍史瓦西解和罗伯逊-沃克模型,以及它们在广义相对论中的重要性。
参考资料
参考资料




Moonshot回答
史瓦西解和罗伯逊-沃克模型是广义相对论中非常重要的两个解。
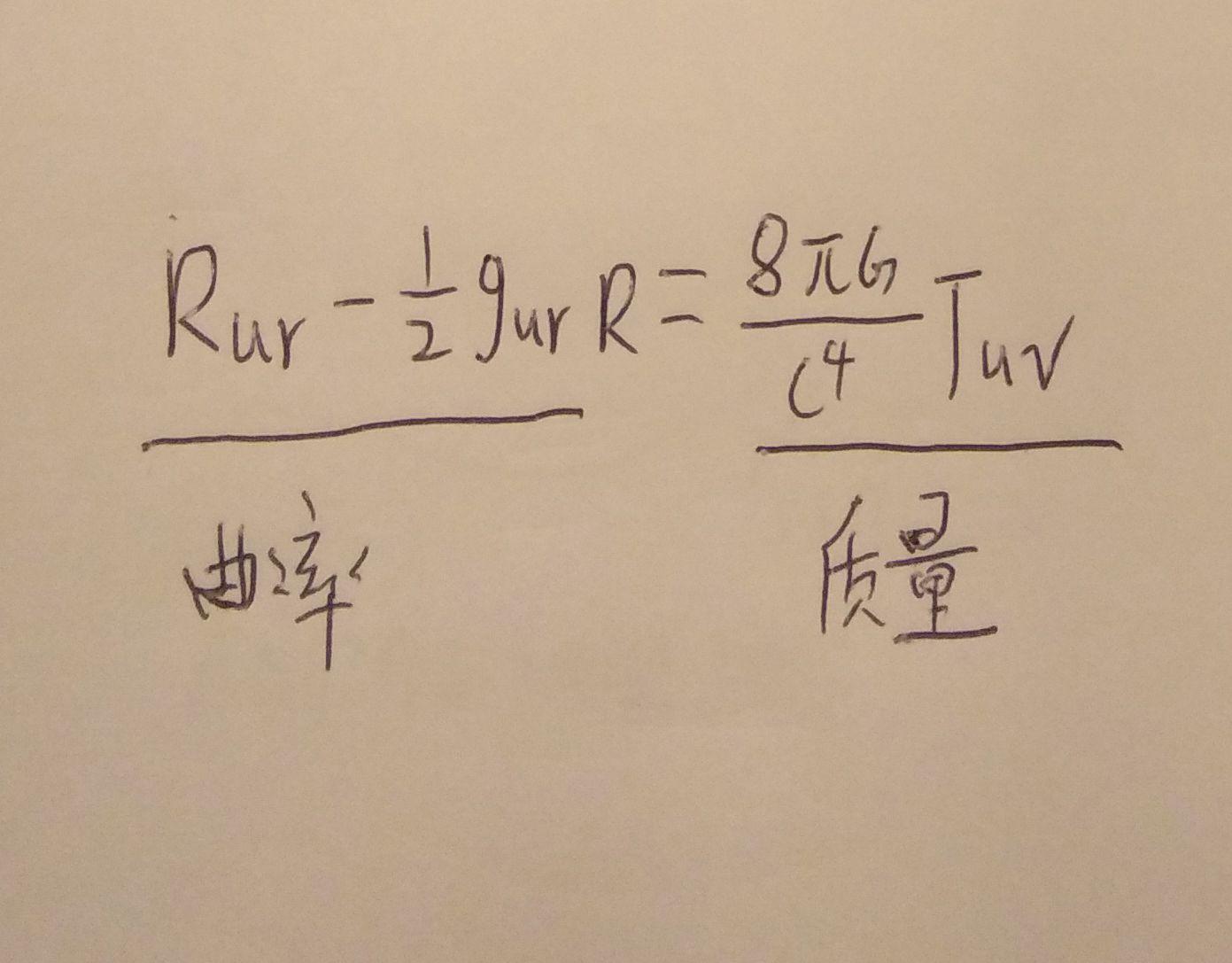
史瓦西解是广义相对论中的第一个严格解,由天文学家史瓦西在1915年求出。这个解描述了球对称质量分布(如非旋转黑洞)所产生的引力场。根据史瓦西解,一个物体的引力场只取决于它的总质量,并且这个解是爱因斯坦场方程在球对称真空中的最一般解。史瓦西解在天体物理学中非常重要,因为它是描述黑洞外部时空结构的基础。此外,史瓦西解还引出了史瓦西半径的概念,这是描述黑洞事件视界的关键参数。
罗伯逊-沃克模型是描述宇宙大尺度结构的度规,由罗伯逊和沃克在20世纪30年代提出。这个模型基于宇宙学原理,即在宇宙的大尺度上,物理条件是均匀且各向同性的。罗伯逊-沃克度规是弗里德曼-勒梅特-罗伯逊-沃克(FLRW)度规的一部分,它与弗里德曼方程一起构成了现代宇宙学的基础。FLRW度规使我们能够讨论宇宙的膨胀和演化,对于理解宇宙的历史和未来至关重要。
这两个解在广义相对论中的重要性在于,它们提供了描述强引力场和宇宙大尺度结构的数学工具。史瓦西解帮助我们理解了黑洞和中子星等致密天体的物理特性,而罗伯逊-沃克模型则为研究宇宙的起源、结构和演化提供了理论基础。通过这些模型,科学家们能够对宇宙进行观测和实验,验证广义相对论的预测。