单位脉冲响应函数在杜哈梅积分中的作用是什么?
参考资料


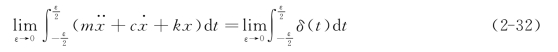
Moonshot回答
单位脉冲响应函数在杜哈梅积分中扮演着核心角色。它表示当系统受到一个单位脉冲(狄拉克δ函数)作用时的响应。这个响应函数可以用来计算系统在任意外载激励下的响应,通过将外载激励函数与单位脉冲响应函数进行卷积运算。具体来说,如果系统受到连续力函数f(t)的作用,其响应可以通过杜哈梅尔积分来求得,即对f(t)与单位脉冲响应函数h(t)的卷积进行积分。这种方法在结构动力学中非常重要,因为它允许工程师计算在一般荷载作用下结构的时域响应。单位脉冲响应函数的求解可以通过频域分析,即通过对频域响应函数H(ω)进行傅里叶逆变换来获得。这种方法不仅适用于理论分析,也适用于实际工程问题,如地震工程和机械振动等领域。