在狭义相对论中,角动量是如何定义和计算的,与经典定义有何不同?
参考资料


参考资料

Moonshot回答
在狭义相对论中,角动量的定义和计算与经典力学有所不同。根据搜索结果,我们可以总结如下:
-
狭义相对论中的角动量:
- 相对论角动量是角动量在狭义相对论与广义相对论中的数学形式与物理概念,与传统经典力学中的角动量有些许差异。
- 相对论角动量考虑了洛伦兹变换,其中四维动量(能量和动量的四维矢量)和四维位置矢量(时间和空间坐标的四维矢量)被用来定义角动量。
- 相对论角动量的定义涉及到四维空间中的内积和外积,这与经典力学中的叉积定义不同。
-
经典力学中的角动量:
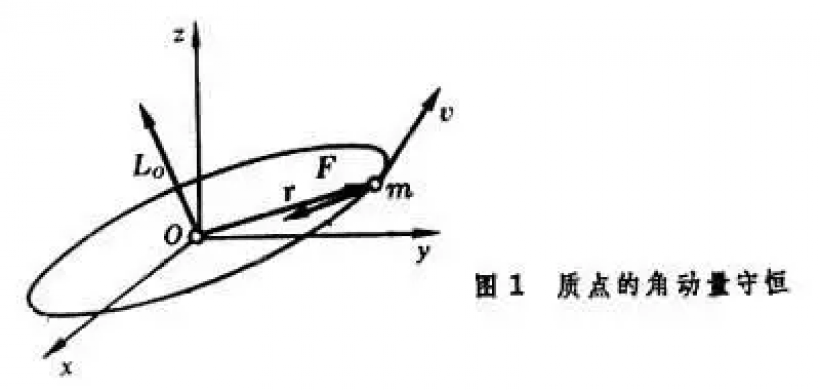
- 在经典力学中,一个粒子对某一点(如原点)的角动量定义为位置矢量和动量矢量的叉积,即 (\vec{L} = \vec{r} \times \vec{p})。
- 经典力学中的角动量是一个三维空间中的矢量,描述了物体的旋转状态和对旋转变化的抵抗力。
-
主要区别:
- 狭义相对论中的角动量是一个四维空间中的概念,而经典力学中的角动量是一个三维空间中的概念。
- 相对论角动量考虑了物体在高速运动时的相对论效应,如时间膨胀和长度收缩,而经典力学中的角动量则假设这些效应可以忽略不计。
- 相对论角动量的守恒不仅适用于孤立系统,还与系统的对称性有关,而经典力学中的角动量守恒通常只考虑孤立系统。
总的来说,狭义相对论中的角动量定义更加复杂,需要考虑相对论效应和四维空间的性质,而经典力学中的角动量定义则更加直观和简单。这些区别反映了物理学从经典到相对论的演变和发展。