参考资料

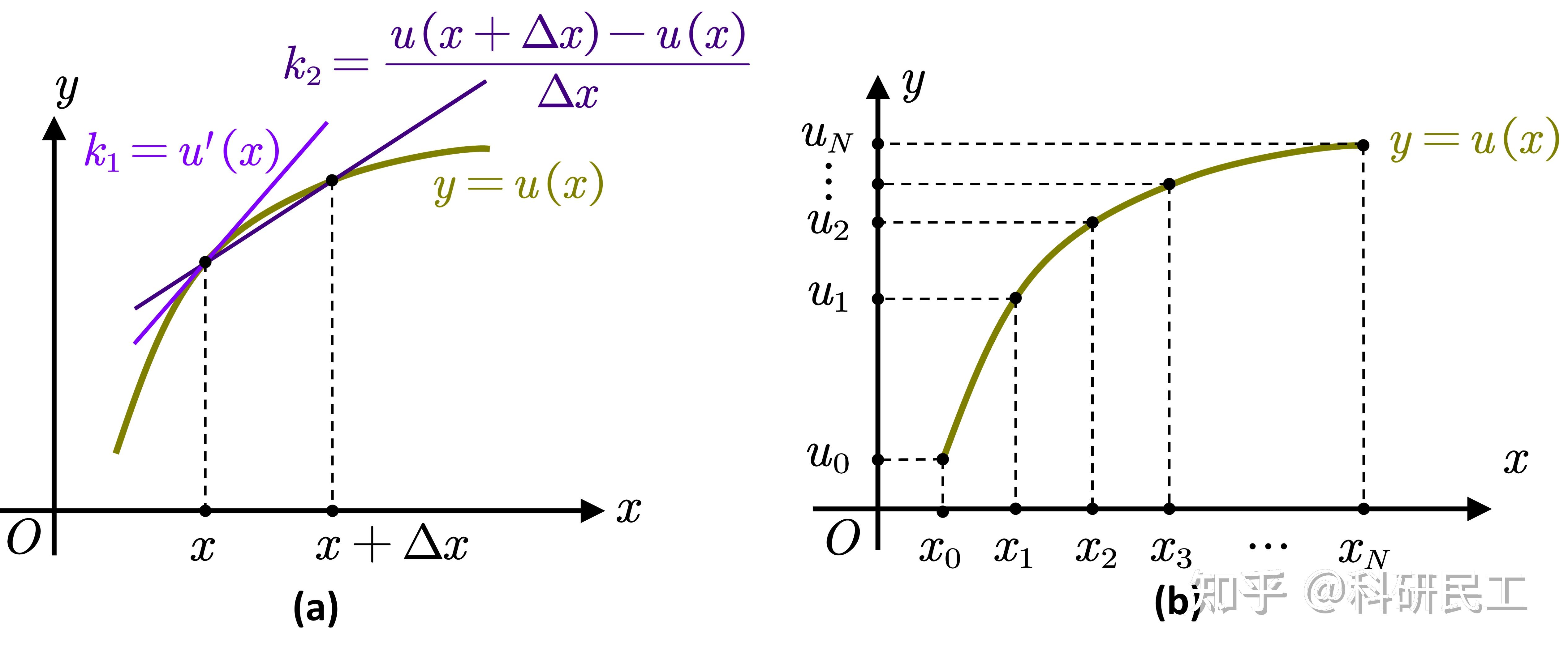
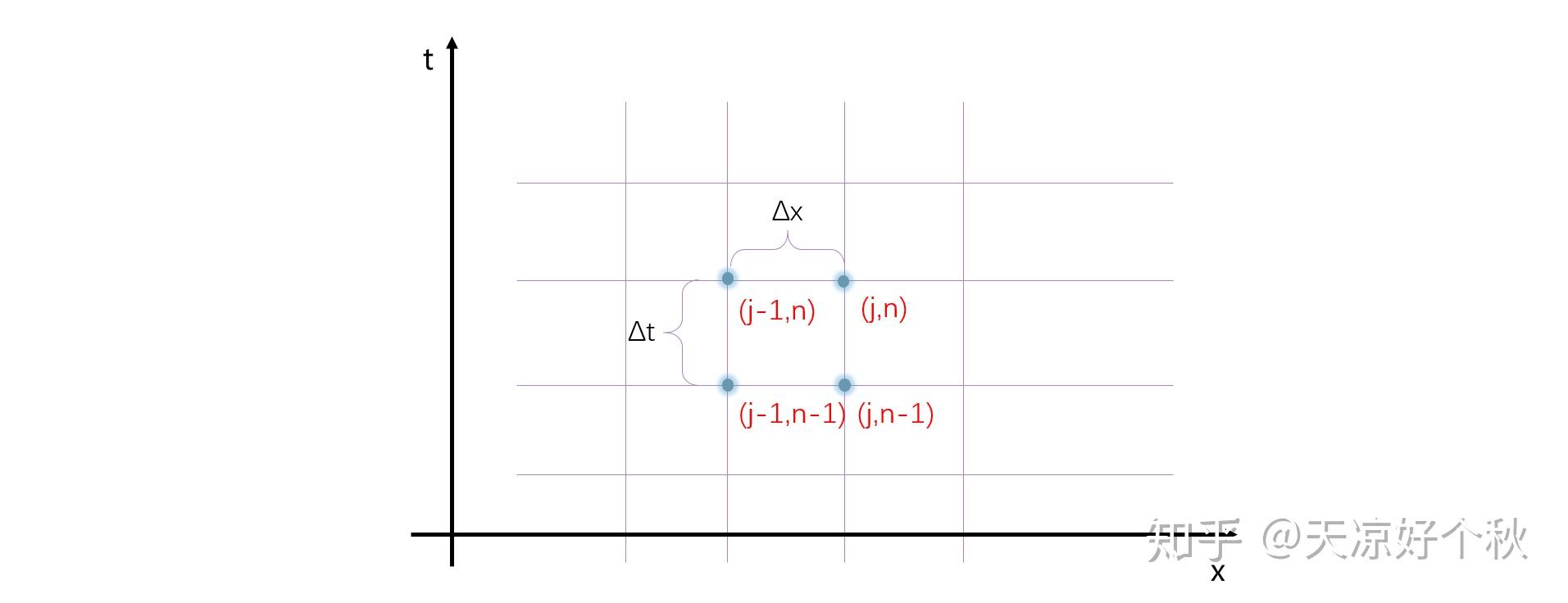
有限差分法是一种在数值分析和计算中广泛使用的近似方法，主要用于求解微分方程的数值解。它通过将微分方程中的微分项用差分的形式来近似，从而将连续的微分方程转化为一组可以数值求解的代数方程。这种方法的原理简单，易于实现，并且计算效率高。

有限差分法在数值分析和计算中的作用包括：

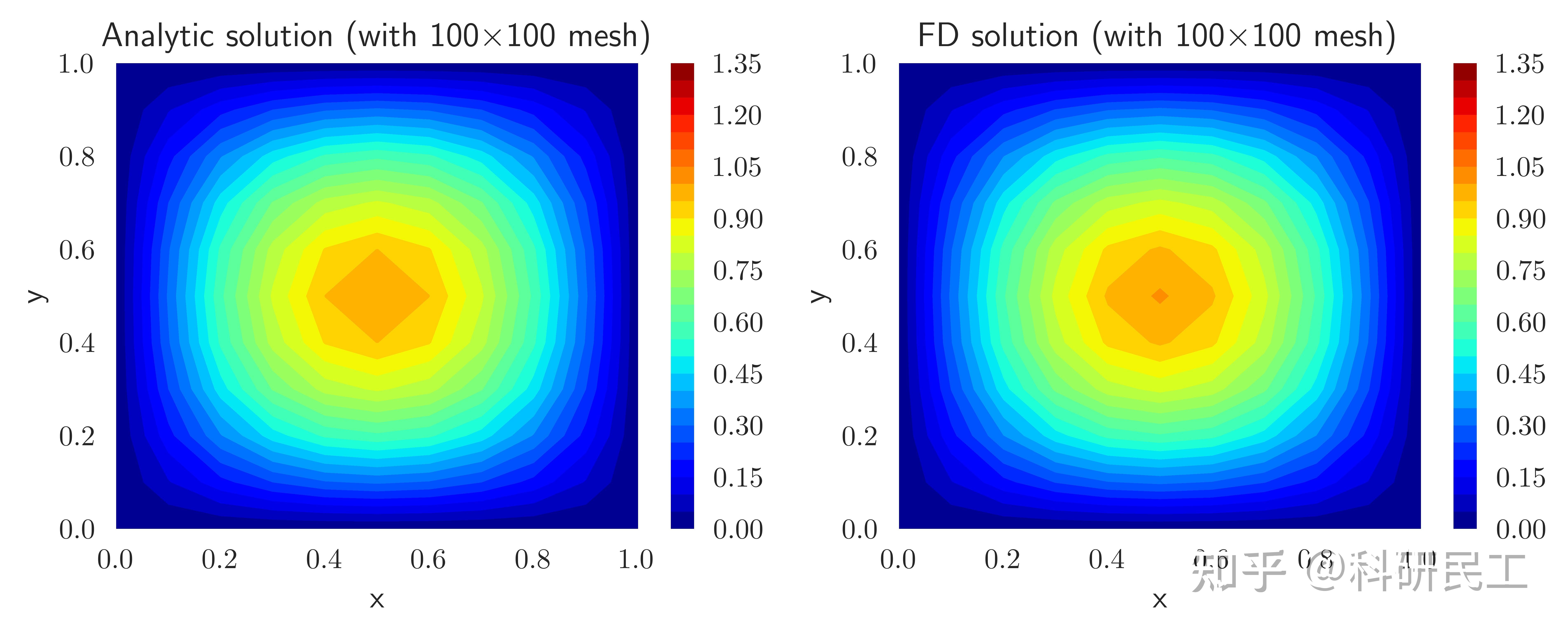
1. 求解偏微分方程：有限差分法可以处理各种类型的偏微分方程，如抛物型、椭圆型和双曲型方程。
2. 近似计算函数导数：在实际应用中，我们常常需要近似计算函数的导数，有限差分法提供了一种简便且有效的方法。
3. 处理复杂边界条件：有限差分法能够处理具有复杂边界条件的问题，使其在工程和物理领域中非常有用。

此外，有限差分法还具有易于编程实现和对计算资源要求相对较低的优点。它在流体动力学、热传导、电磁学、量子力学等领域都有广泛的应用。

以下是一些与有限差分法相关的图像，可以帮助直观理解其概念和应用：

更多详细信息可以参考以下资源：

• 有限差分法的基本流程与常用格式
• 微分方程数值解法|专题（1）——常微分方程的有限差分方法
• 微分方程数值解法|专题（2）——偏微分方程的有限差分方法