参考资料

波义耳-马略特定律在气体理论中非常重要，原因如下：

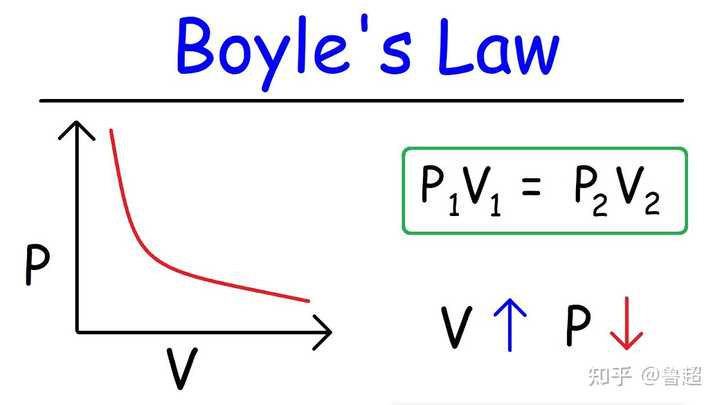
1. 描述理想气体行为：波义耳-马略特定律表明，在恒温条件下，一定质量的理想气体的体积与压强成反比。这一定律是描述理想气体状态的基本关系之一，为理解和预测气体行为提供了一个简单而准确的模型。

2. 理想气体状态方程的基础：波义耳-马略特定律是理想气体状态方程 ( pV = nRT ) 的一个组成部分，该方程是描述理想气体状态的四个基本物理量（压强p、体积V、温度T和摩尔数n）之间关系的方程。它在工程、化学和物理学中有广泛的应用。

3. 实验验证和科学方法的典范：波义耳和马略特通过实验独立发现了这一定律，展示了科学方法的力量。他们的工作为后来的科学家提供了实验验证和理论推导的范例。

4. 对其他气体定律的启示：波义耳-马略特定律与查理定律和盖·吕萨克定律一起，为综合气体定律奠定了基础，该定律进一步描述了在变化的温度和体积下气体压强的变化。

5. 实际应用广泛：在工程、气象学、化学工业、呼吸生理学等领域，波义耳-马略特定律都是理解和预测气体行为的重要工具。

6. 教育价值：作为热力学和气体物理学的基础知识，波义耳-马略特定律是科学教育中不可或缺的一部分，帮助学生建立起对气体状态和行为的基本理解。

波义耳-马略特定律的这些重要性，不仅体现在理论上，也体现在其广泛的实际应用中。定律的简单性和普适性使其成为理解和操作气体系统的关键。