参考资料

参考资料


Moonshot回答
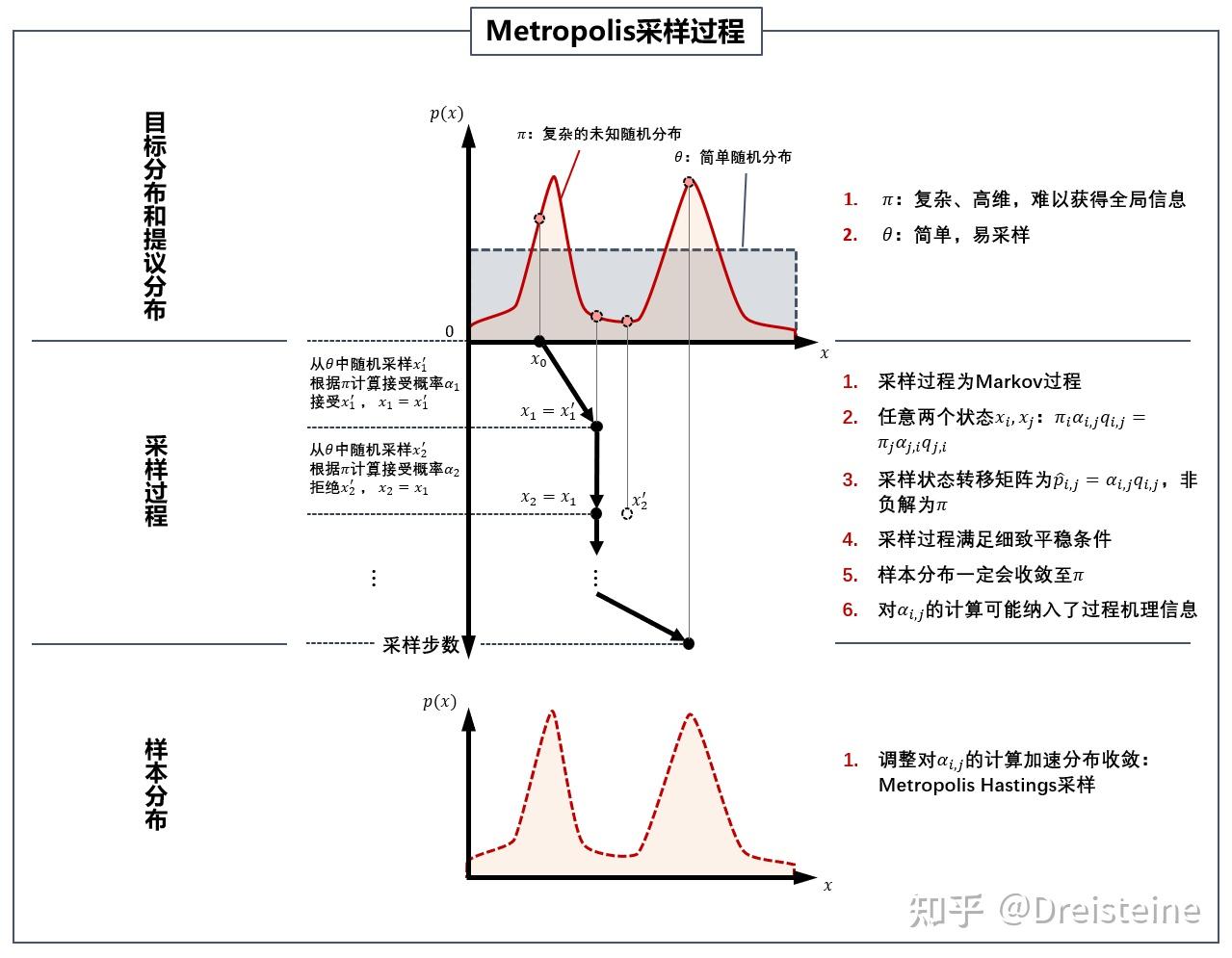
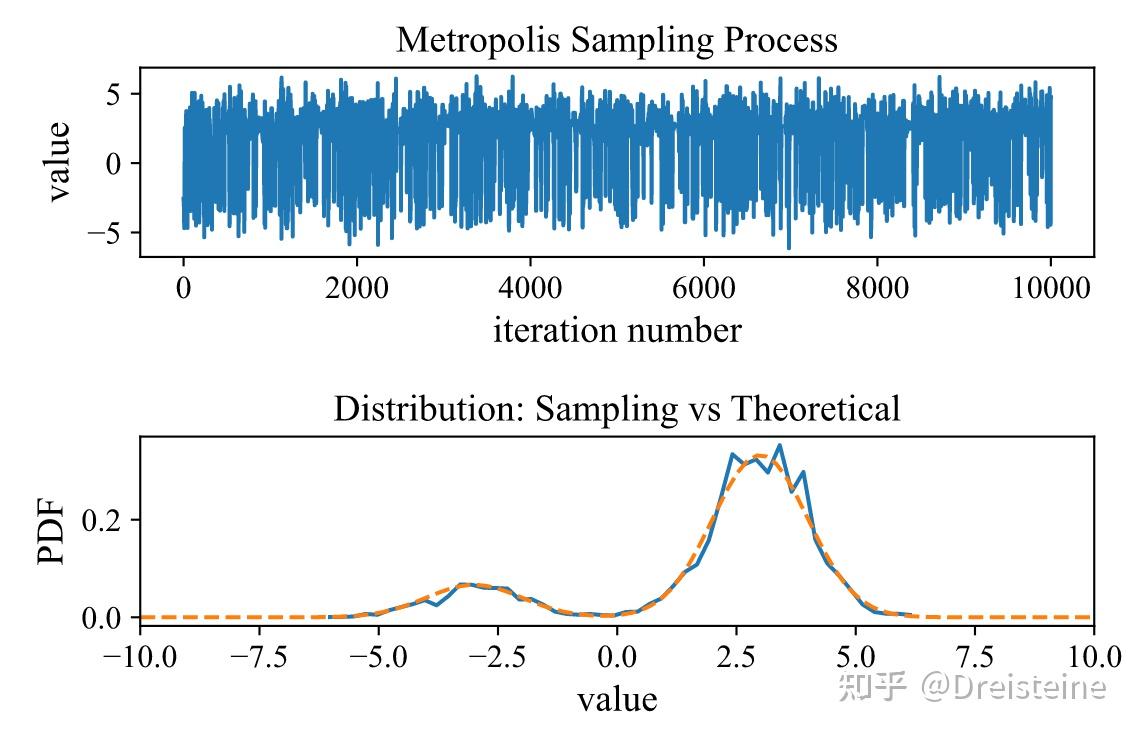
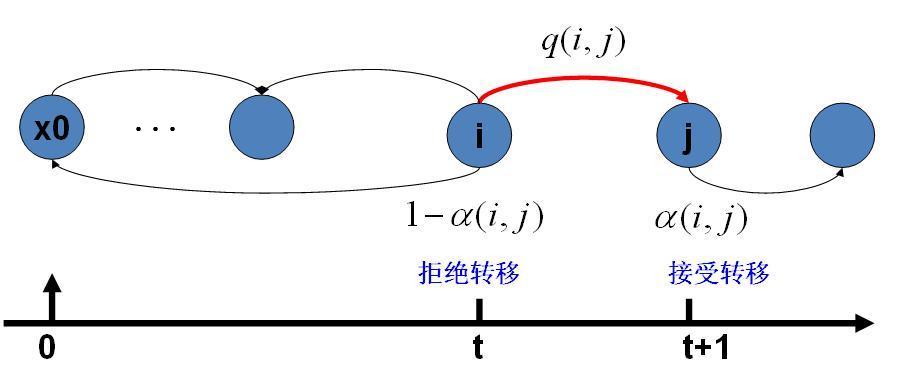
Metropolis算法是一种马尔可夫链蒙特卡洛(MCMC)方法,用于从概率分布中生成样本序列。它由Metropolis等人在1953年提出,最初用于统计力学。算法的工作原理是通过构建一个马尔可夫链,使其平稳分布等于目标分布。算法步骤包括:
- 从当前状态μ选择一个邻近状态ν。
- 计算接受概率A(μ, ν),如果新状态的能量低于当前状态,则接受概率为1,否则根据能量差计算接受概率。
- 生成一个[0,1]之间的随机数r,如果r小于接受概率A(μ, ν),则接受新状态ν,否则保持当前状态μ。
- 重复以上步骤,直到生成足够数量的样本。
在易辛模型中,Metropolis算法被用来研究磁系统的相变和临界现象。易辛模型是一个描述磁体中原子磁矩相互作用的模型,其哈密顿量H(σ)通常表示为:
[ H(\sigma) = -\sum_{<i~j>} J_{ij} \sigma_i \sigma_j ]
其中,σ_i和σ_j是相邻原子的磁矩,J_ij是相互作用常数。在模拟过程中,Metropolis算法通过随机改变磁矩的指向来生成一系列状态,从而模拟系统的热力学性质。
根据搜索结果,Metropolis算法在易辛模型中的应用包括使用Metropolis-Hastings算法进行数值模拟,以及与其他算法如Swendsen-Wang和Wolff算法进行比较。Wolff算法被认为是最好的聚类翻转Monte-Carlo算法,而Metropolis和Swendsen-Wang算法理论上也适用于易辛模型的模拟。此外,易辛模型的维基百科页面提供了关于模型的详细信息,包括其定义、性质和应用。
这张图展示了易辛模型中原子磁矩的相互作用,其中相邻原子的磁矩要么同向(红色),要么反向(蓝色),Metropolis算法通过随机改变磁矩的指向来模拟系统的热力学性质。
继续提问
相关问题
为何乐观和希望在激励穷人实现长期目标和摆脱贫困方面发挥重要作用?
什么是单晶纤维,雷射加热平台成长技术在单晶纤维生产中的作用是什么?
为什么北京大兴国际机场被誉为“新国门”?
为什么新西兰成为世界上第一个女性获得投票权的国家?
温哥华影评人协会奖的最佳电影奖项评选的标准是什么?
圣安东尼奥马刺在2006-07 NBA赛季总决赛中是如何以4:0的比分击败克里夫兰骑士的?他们的关键策略是什么?
雪农·波瑟因在Netflix哪部电视剧中首次亮相,并因此获得了黄金时段艾美奖提名?
公元535年至554年的哥德戰爭,拜占庭帝國是如何最終擊敗東哥德王國的?
特别版 Free! -Take Your Marks-的剧情大致讲述了哪些内容?
彼得·彼得罗维奇·格列博夫因主演哪部电影而深得克列日涅夫的喜爱?