向量外积的结果是什么类型的向量,其三个标量元素具体是如何计算的?
参考资料



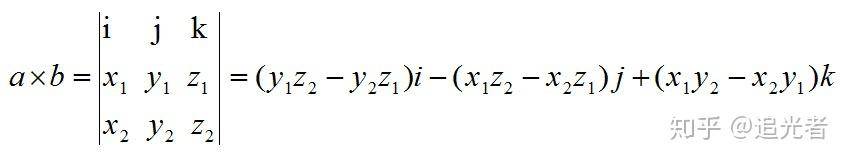
参考资料
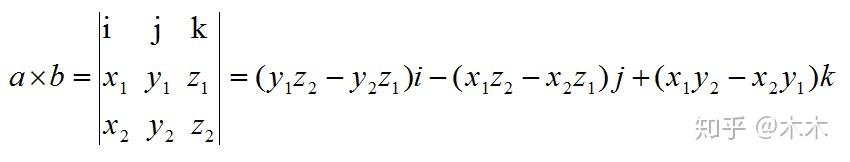



Moonshot回答
向量的外积,也称为张量积,其结果是一个矩阵。具体来说,给定两个向量 (\mathbf{a}) 和 (\mathbf{b}),其中 (\mathbf{a}) 是一个 (m \times 1) 的列向量,而 (\mathbf{b}) 是一个 (1 \times n) 的行向量,它们的外积 (\mathbf{a} \otimes \mathbf{b}) 将得到一个 (m \times n) 的矩阵。这个矩阵的每个元素 (C_{ij}) 是通过将向量 (\mathbf{a}) 的第 (i) 个元素与向量 (\mathbf{b}) 的第 (j) 个元素相乘得到的,即 (C_{ij} = a_i \cdot b_j)。
对于三维空间中的两个向量 (\mathbf{a} = (a_1, a_2, a_3)) 和 (\mathbf{b} = (b_1, b_2, b_3)),它们的外积结果将是一个 (3 \times 3) 的矩阵,其标量元素计算如下: [ \begin{bmatrix} a_1b_1 & a_1b_2 & a_1b_3 \ a_2b_1 & a_2b_2 & a_2b_3 \ a_3b_1 & a_3b_2 & a_3b_3 \ \end{bmatrix} ]
这种运算在物理学和工程学中非常有用,例如在描述两个向量构成的平面的法向量或者在构建坐标系时。外积也可以视为克罗内克积的一种特例。更多信息可以参考 维基百科。