如何通过高斯函数构造双曲函数形式的星积公式?
参考资料
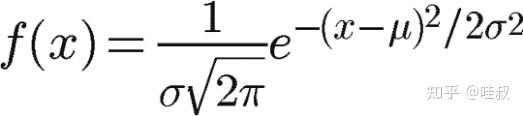


Moonshot回答
要通过高斯函数构造双曲函数形式的星积公式,首先需要了解双曲函数与高斯函数之间的关系。双曲函数可以用指数函数来定义,例如双曲正弦函数 (\sinh(x) = \frac{e^x - e^{-x}}{2}) 和双曲余弦函数 (\cosh(x) = \frac{e^x + e^{-x}}{2})。这些定义与高斯函数 (e^{-x^2}) 有相似之处,因为它们都是由指数函数构成。
在构造星积公式时,可以考虑使用高斯函数的性质,例如其在傅里叶变换中的重要作用。高斯函数在傅里叶变换中具有不变性,即变换后的函数仍然是高斯函数。这一性质可以用于构造双曲函数形式的星积公式,通过将双曲函数与高斯函数结合,利用傅里叶变换的性质来推导星积公式。
此外,双曲函数在积分技巧中也有应用,例如在处理形如 (\sqrt{x^2 \pm a^2}) 的被积函数时,可以使用双曲代换 (x = \sinh(t)) 或 (x = \cosh(t)) 来简化积分过程。这种技巧可能对构造星积公式有所启发。
综上所述,通过结合高斯函数的性质和双曲函数的积分技巧,可以探索构造双曲函数形式的星积公式。具体的构造方法可能需要更深入的数学推导和分析。