参考资料

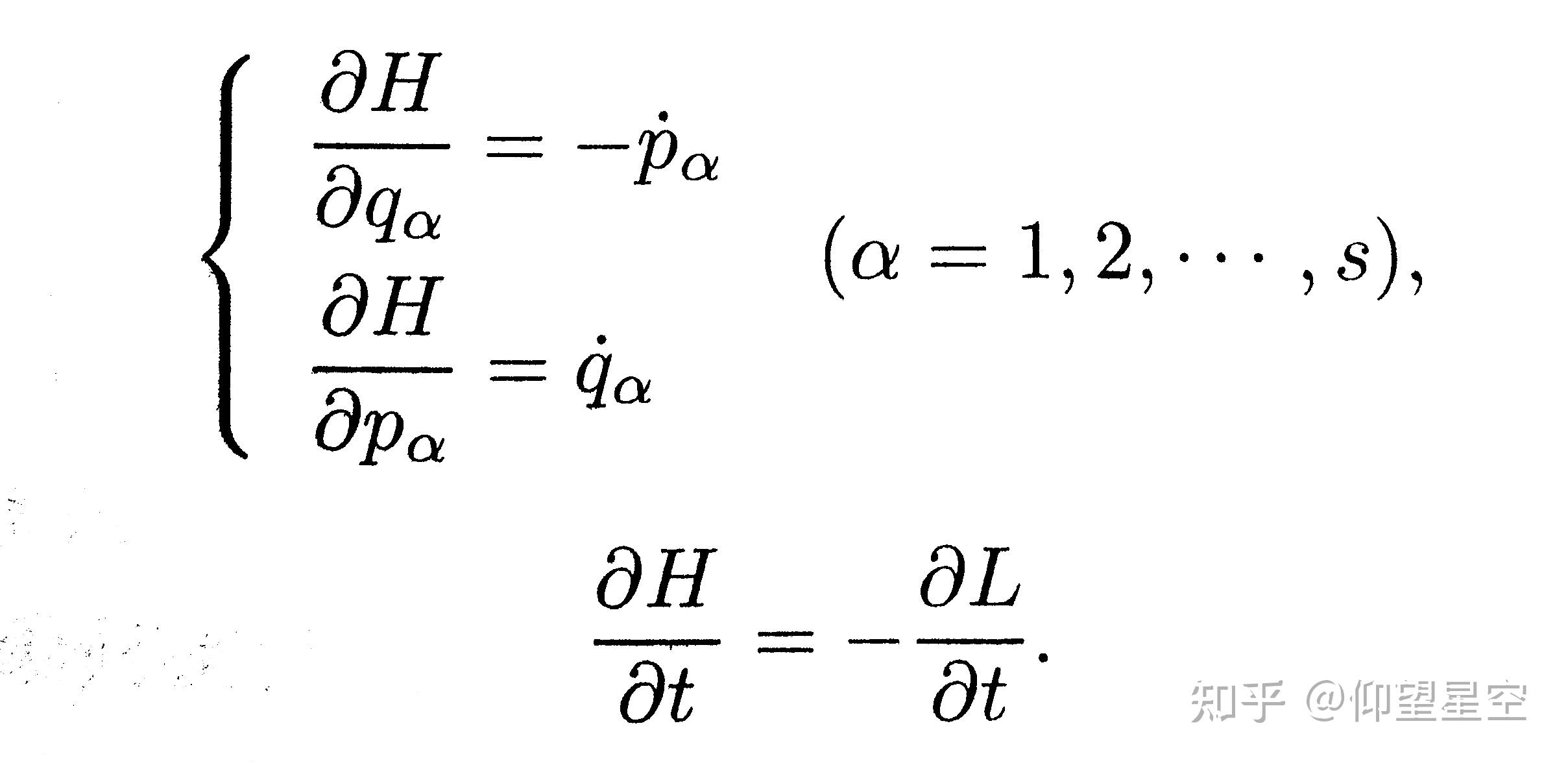

Moonshot回答
通过哈密顿特征函数求出动力学系统的运动常数,可以遵循以下步骤:
-
建立哈密顿函数:首先需要确定系统的哈密顿量 (H),它通常表示为广义坐标 (q_i)、广义动量 (p_i) 和时间 (t) 的函数,即 (H(q_i, p_i, t))。
-
写出哈密顿方程:根据哈密顿函数,写出该系统的哈密顿方程,即: [ \dot{q}_i = \frac{\partial H}{\partial p_i}, \quad \dot{p}_i = -\frac{\partial H}{\partial q_i} ] 其中,点表示时间导数。
-
求解哈密顿方程:求解这些方程以找到系统的运动方程。这可能需要使用数值方法或解析方法,具体取决于系统的复杂性。
-
识别守恒量:在哈密顿系统中,运动常数通常与守恒量相关。例如,如果哈密顿量不显式依赖于时间,则能量是守恒的。如果哈密顿量不依赖于某个坐标,则相应的广义动量是守恒的。
-
利用刘维尔定理:刘维尔定理指出,相空间的分布函数沿着系统的轨迹是常数。这意味着如果能找到系统的一个不变量(比如能量),那么这个不变量可以作为运动常数。
-
分析系统的动力学行为:通过研究哈密顿系统从规则到混沌的过渡,可以进一步理解系统的动力学行为和可能的守恒量。
以上步骤结合了从哈密顿力学的基本概念到具体的动力学分析。通过这些步骤,可以系统地求出动力学系统的运动常数。同时,可以参考维基百科上的哈密顿力学和刘维尔定理条目,以及知乎上关于哈密顿力学的专栏文章,来获取更深入的理解。
继续提问
相关问题
纳粹德国在第二次世界大战中的扩张策略是什么?
吴如愚的著作《准斋杂说》有哪些主要内容和核心思想,为什么在清代会佚失?
赫倾文在电视剧《幸福专卖店》中饰演的是什么角色?
舒淇代言过哪些品牌的产品,在代言领域中她有哪些代表性的广告代言?
范仲淹在1043年提出的《答手詔條陳十事》对北宋产生了怎样的影响?
股票长期价值如何能在短期市场波动中被合理评估,以帮助投资者做出更精准的投资判断?
古代墨西哥的天文学家是如何观测天空的?
625年,希拉克略在对抗萨珊王朝的战争中取得了哪些重要胜利?
格雷格·弗萊瑟在《曼達洛人》中使用了哪些特殊的摄影技术,使他获得了艾美奖最佳连续剧摄影奖?
在婚姻仪式中,为什么集体筹集婚礼补偿金是重要的文化实践?