参考资料



参考资料




Moonshot回答
共形场论(Conformal Field Theory,简称CFT)是一种特殊的量子场论,它在共形变换下保持不变。共形变换是一种角度保持不变的变换,例如放缩和旋转,但不允许有反射。在二维情况下,共形场论有一个局部共形变换的无限维代数,这使得它有时可以被精确求解或分类。共形场论在多个领域有重要应用,包括凝聚态物理学、统计力学、量子统计力学以及弦论。
在世界面上运用共形场论,通常涉及到考虑一个带有边界的空间,并且定义在该边界上满足共形不变条件的场论。这种理论被称为边界共形场论(Boundary Conformal Field Theory)。边界共形场论在处理临界现象和统计模型的边界效应时非常有用,例如在研究开弦理论时,开弦的端点就位于这样的边界上。
共形场论的核心问题之一是如何利用共形对称对所有的CFT进行求解和分类。对于高维的CFT,共形对称本身可能并不足够,需要结合其他对称性或条件来实现。
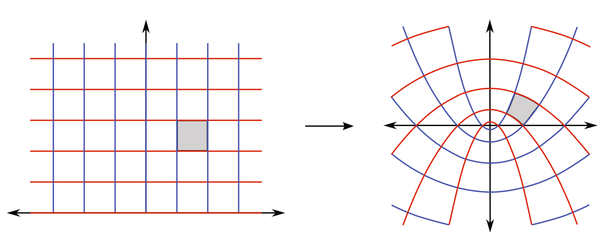
以下是一些与共形场论相关的图片,可以帮助直观理解这一理论:



更多详细信息可以参考维基百科上的共形场论条目。
继续提问
相关问题
蔷薇属植物的种类和分类方法是什么,为什么中国产的种类会有82种之多?
《解救吾先生》这部电影是根据哪一起真实案件改编的?
在希腊岛屿上,除了观光和海滩,还有哪些有趣的活动和体验值得尝试?
公元前13世纪,商朝的哪位君主在位期间被认为是中国历史上的一个重要转折点?
柯瑞贺是否有音乐作品,如果有关请列举其中一首歌名?
俄罗斯远东地区的地缘战略地位为何如此重要?
史蒂夫·哈维主持的《家族问答》节目从何时开始,他还主持过哪些类似的节目?
3D打印技术在锈带制造业复兴中扮演了什么角色?
电影续集制作的主要考虑因素有哪些,市场表现如何影响续集的拍摄决定?
塞斯·罗根和伊凡·戈博合作过哪些喜剧电影,他们之间的合作有哪些亮点?