如何定义一个度量空间的测地线?它与微分几何中的定义有何不同?
参考资料
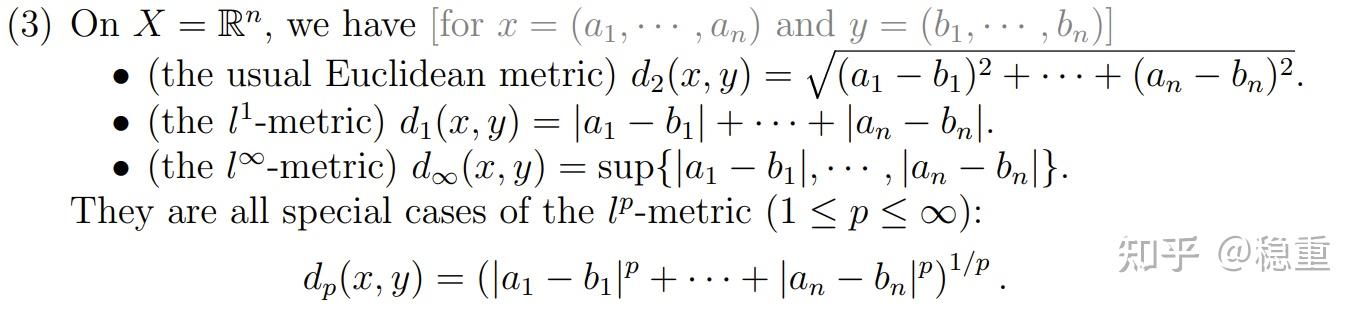

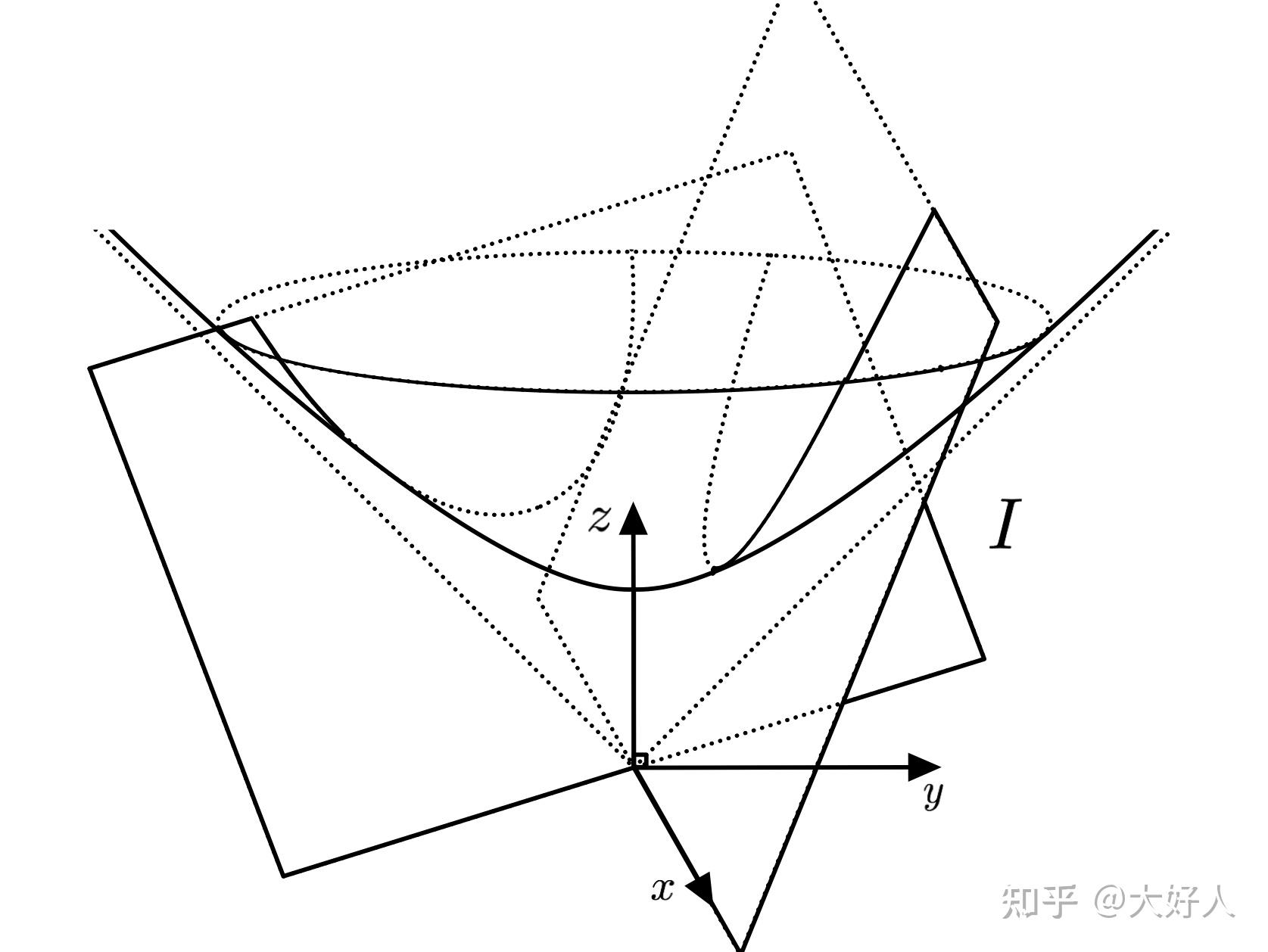
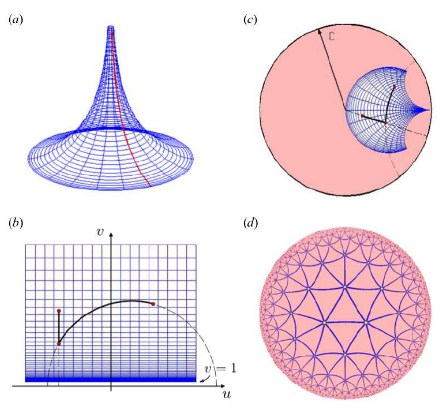
参考资料
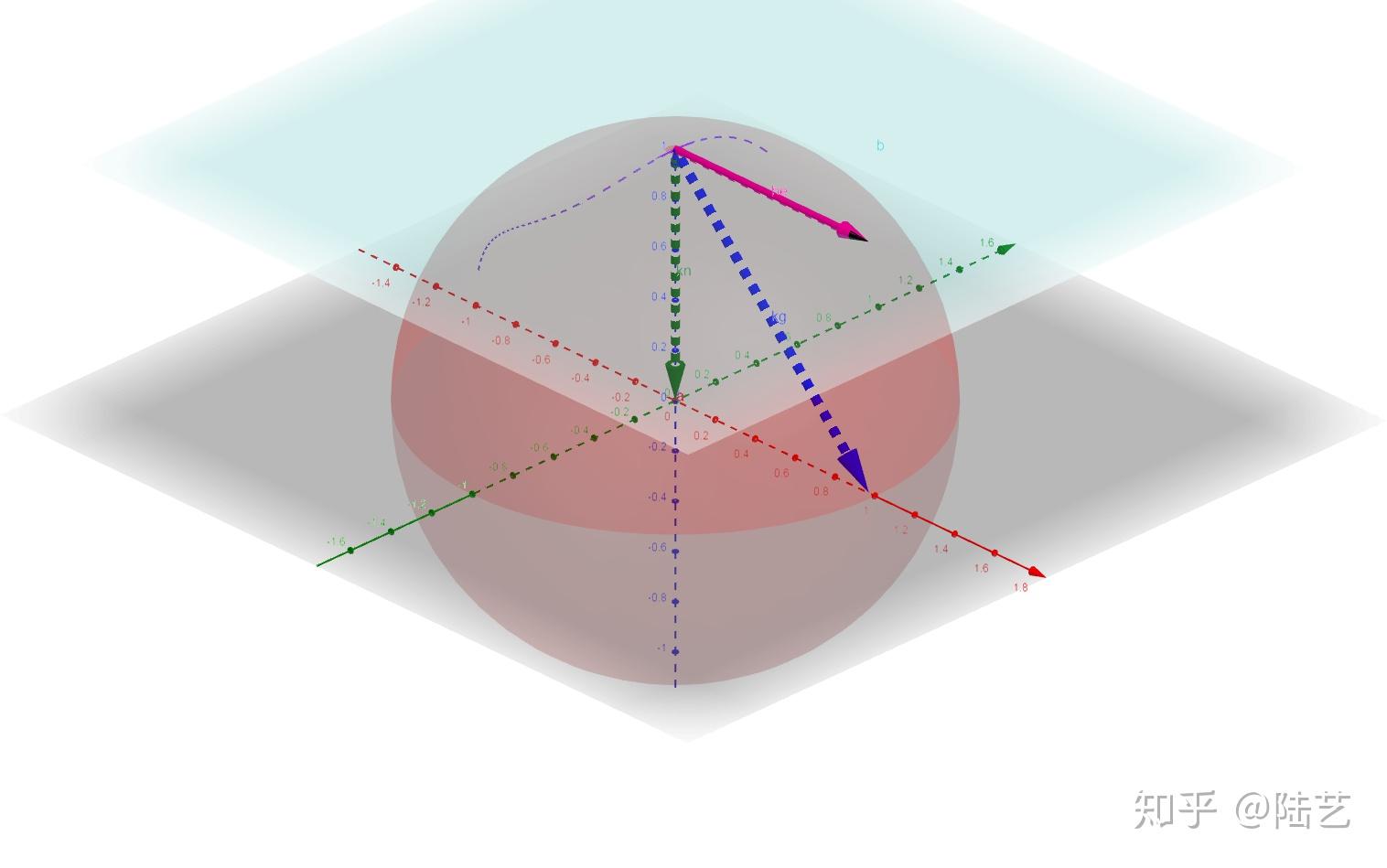



Moonshot回答
在度量空间中,测地线可以定义为局部最短路径,即在任何小区间上都走过度量最短的路径。这个定义依赖于度量空间中存在一个度量,允许我们测量距离。测地线在度量空间中可能不存在或不唯一,这取决于空间的具体结构。
在微分几何中,测地线的定义更加严格,并且与流形的几何结构紧密相关。测地线是一条其切向量沿曲线方向进行平行传输的曲线。这意味着测地线在局部上最小化距离,并且其切向量场是平行的。在微分几何中,测地线的存在性和唯一性通常由流形的度量张量和联络来保证。
度量空间和微分几何中测地线定义的主要区别在于:
- 定义的严格性:微分几何中的定义更加严格,依赖于流形的内蕴结构和平行传输的概念。
- 存在性和唯一性:在微分几何中,给定一个点和该点处的一个切向量,存在唯一的测地线通过该点且具有该切向量。
- 依赖性:度量空间中的测地线依赖于度量的存在,而微分几何中的测地线则依赖于流形的度量张量和联络。
通过搜索结果,我们可以看到度量空间和微分几何中测地线定义的这些区别得到了体现。例如,知乎上的讨论强调了度量空间中测地线可能不存在或不唯一的情况,而微分几何的资料则更侧重于测地线作为平行传输曲线的性质。这些信息帮助我们理解了两种定义之间的联系和差异。