向量叉积和点积在实际应用中有什么不同?请举例说明。
参考资料
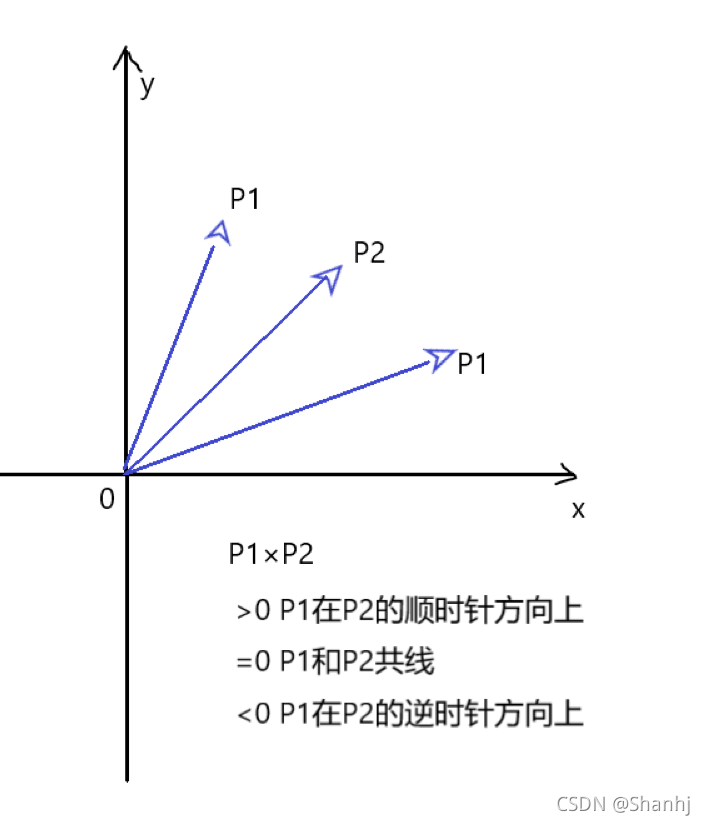

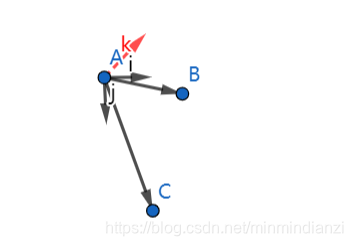
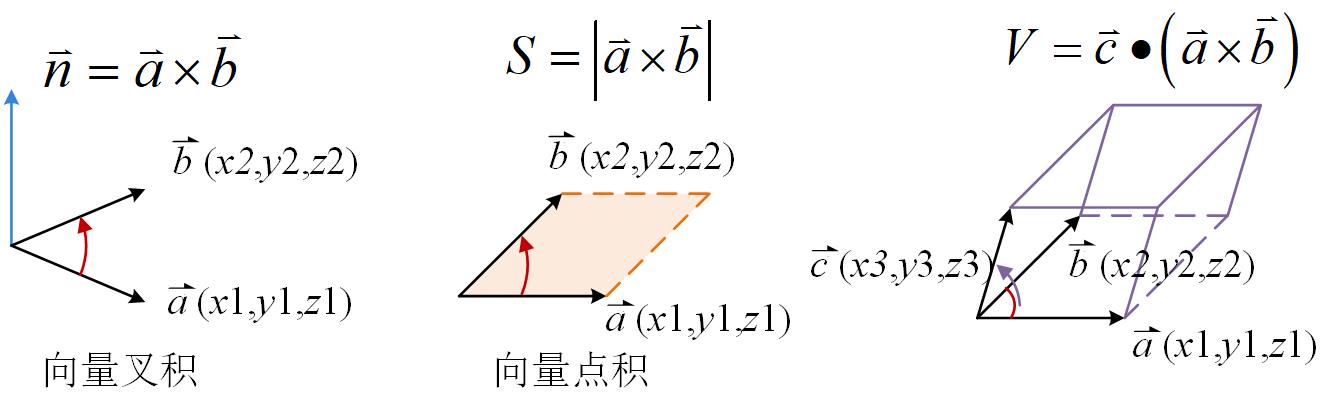
参考资料
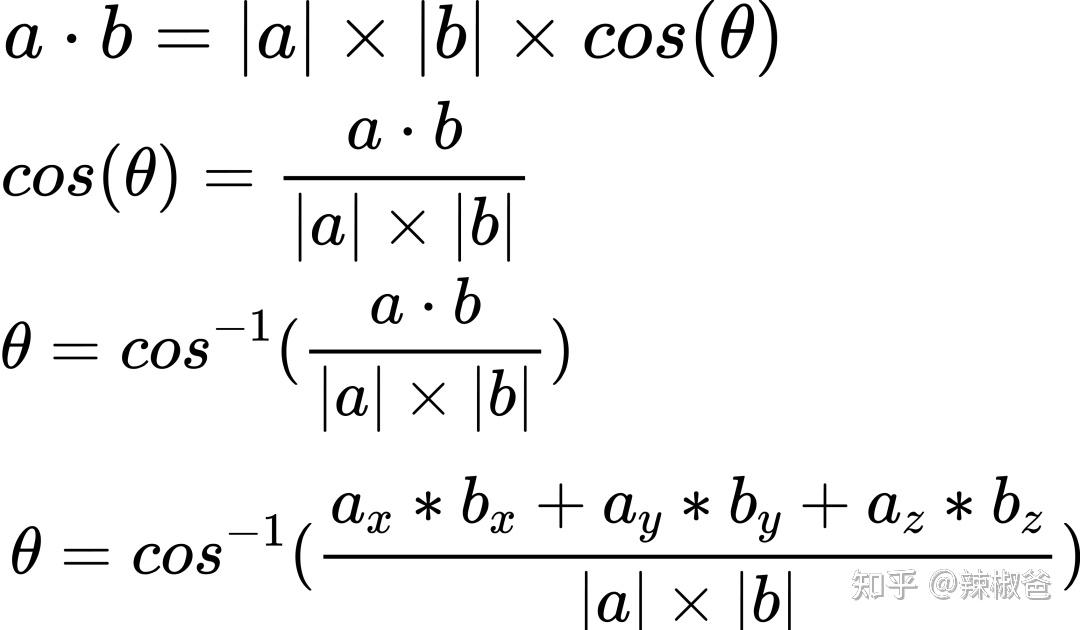
Moonshot回答
向量叉积和点积在实际应用中具有不同的用途和特点。以下是一些具体的例子:
-
向量叉积:
- 应用在物理学中:叉积常用于计算力矩和角动量。例如,一个物体绕轴旋转时,其角动量可以表示为位置向量和动量向量的叉积。
- 计算面积:在计算三角形或多边形的面积时,可以使用构成多边形的两个向量的叉积的模长来计算。例如,三角形的面积可以通过 ( \frac{1}{2} | \vec{AB} \times \vec{AC} | ) 来计算。
- 确定法向量:在计算机图形学中,叉积可以用来确定一个平面的法向量,这对于光照和阴影的计算非常重要。
-
向量点积:
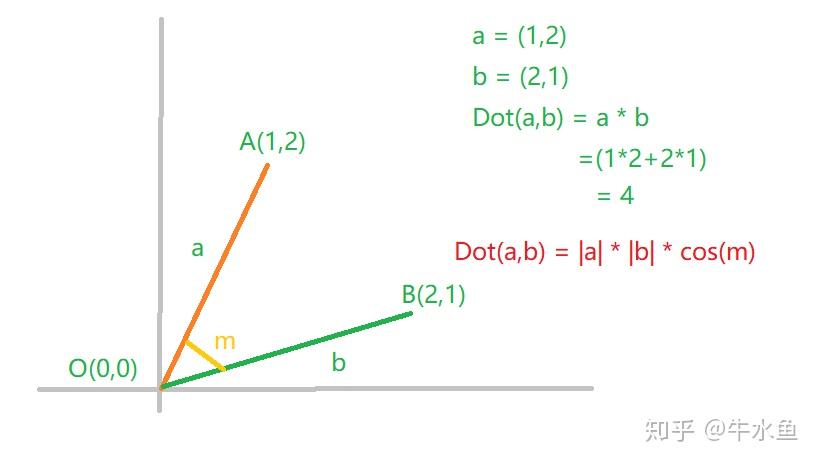
- 计算相似度:在机器学习和数据挖掘中,点积可以用来衡量两个向量的相似度。例如,通过计算两个文档向量的点积,可以判断它们在内容上的相似性。
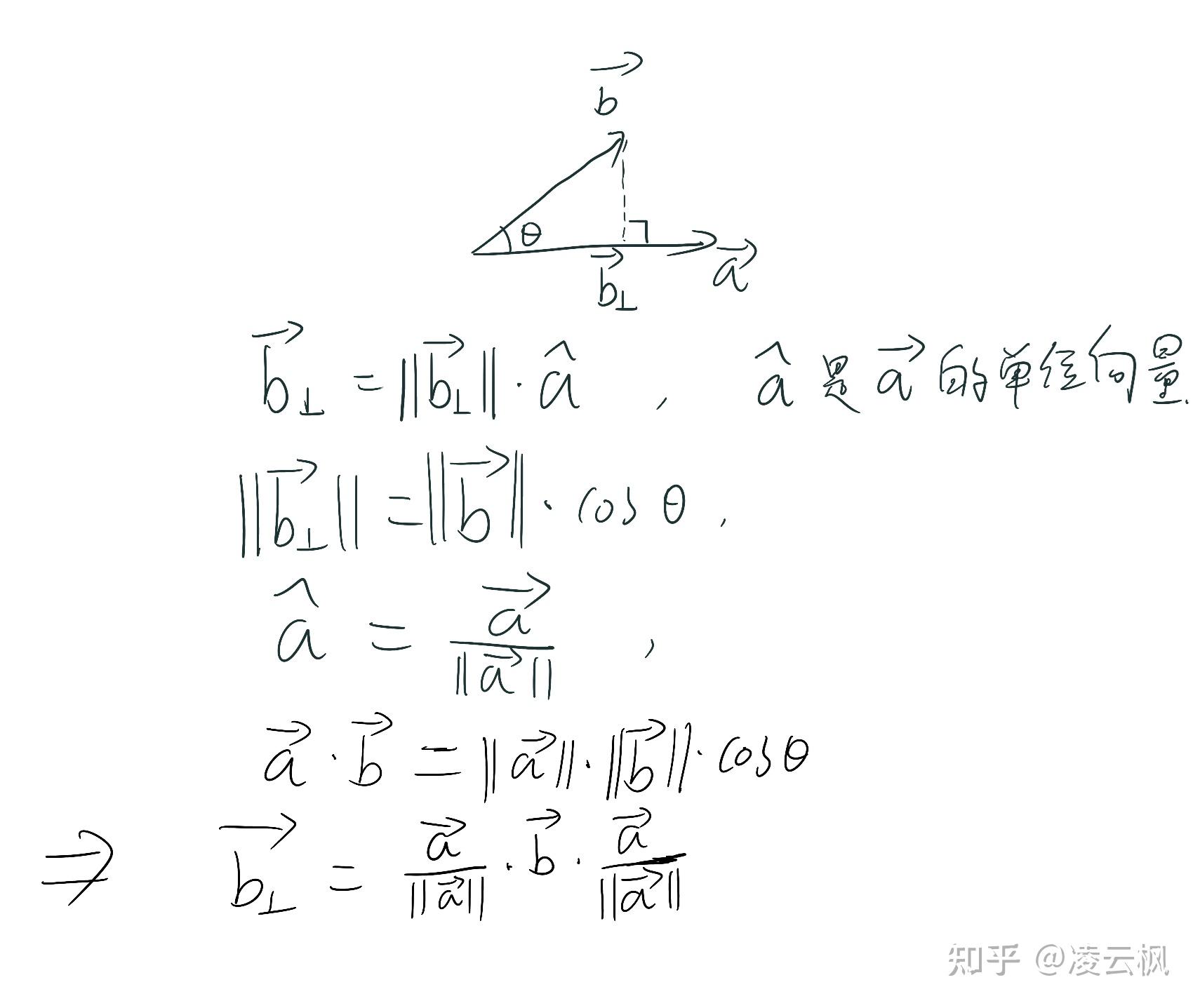
- 投影和反射:在计算机图形学中,点积用于计算一个向量在另一个向量上的投影,这对于光线追踪和物体的反射特性计算非常重要。
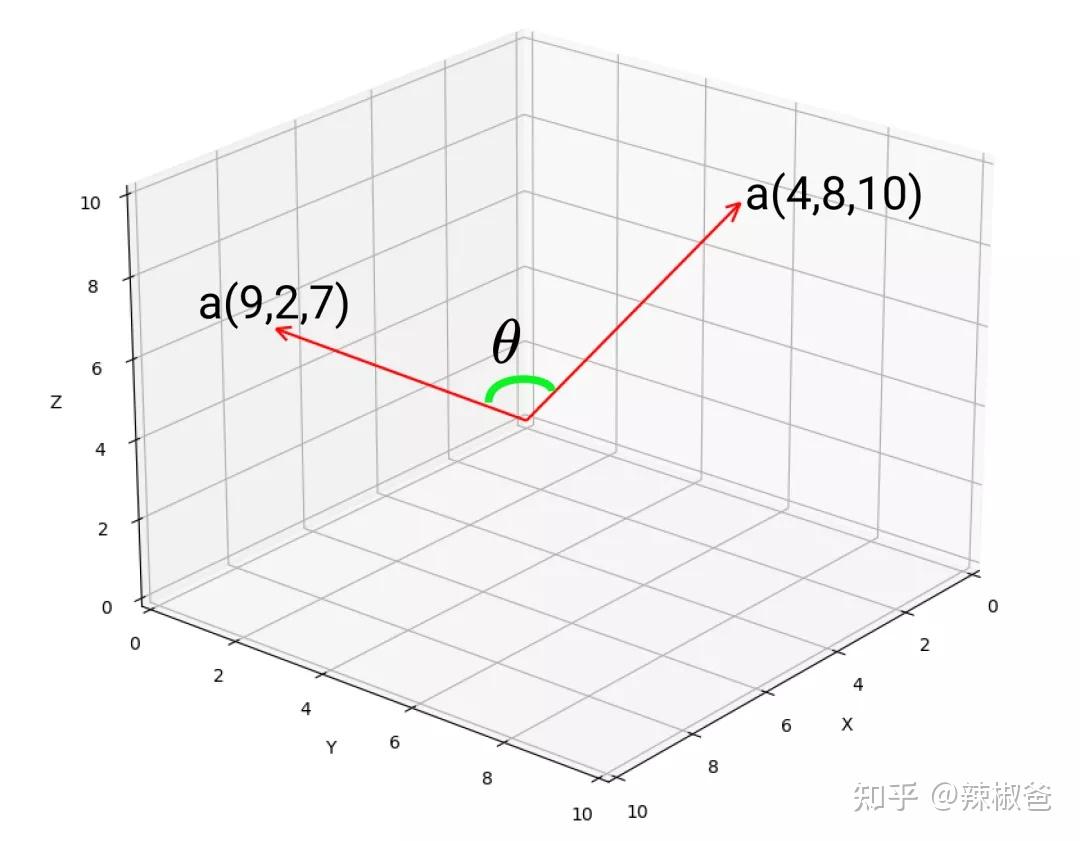
- 余弦定理:点积也用于余弦定理中,计算两个向量之间的夹角,这在物理学和工程学中非常有用。
总的来说,叉积和点积在不同的领域和应用中发挥着关键作用,它们各自独特的数学性质使得它们在解决特定问题时非常有用。叉积通常与垂直性和面积计算相关,而点积则与相似度、投影和角度计算相关。