参考资料

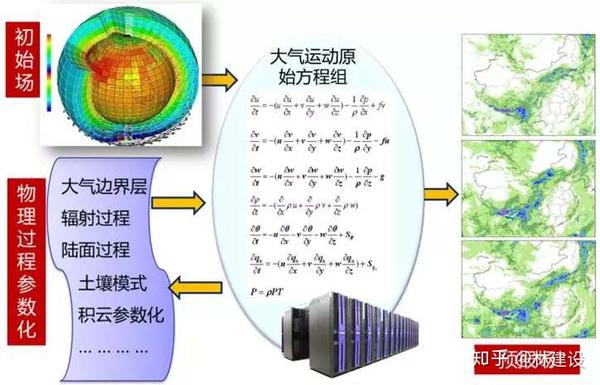
数值天气预报的基本方程式包括：

1. 连续性方程：描述了大气中空气质量的守恒，确保了在没有源或汇的情况下，空气的质量既不会被创造也不会被消灭。
2. 动量方程：描述了大气运动的动量守恒，涉及到风速的变化，包括水平和垂直方向。
3. 热力学方程：描述了大气中能量的守恒，包括温度变化和潜热的转换。
4. 水汽混合比或比湿方程：描述了大气中水汽含量的变化。
5. 状态方程：描述了气压、温度和密度之间的关系。

这些方程在预测中的作用是：

• 描述大气状态：它们提供了大气状态变量（如气压、温度、湿度和风速）之间关系的数学描述。
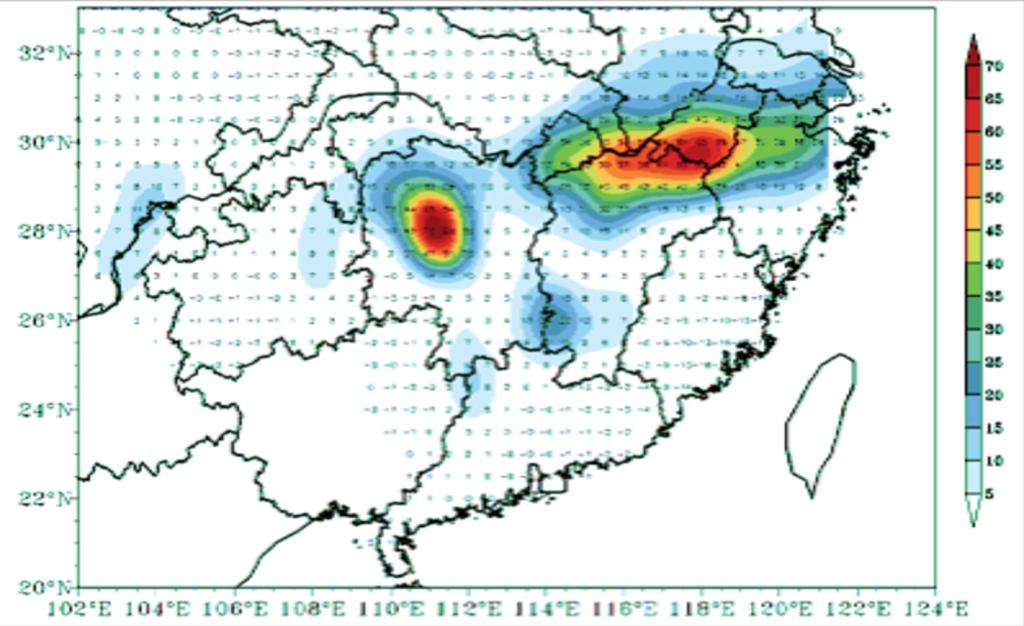
• 预测天气变化：通过求解这些方程，可以预测未来某个时间点的大气状态。
• 物理过程的参数化：对于无法直接解析的物理过程（如湍流、云和降水），通过参数化方案在模型中近似表示。
• 模式初始化和积分：使用观测数据来初始化模型，然后通过数值积分求解方程，得到未来天气的预测。

数值天气预报的发展历史中，如皮耶克尼斯提出的诊断方程，包含了七个变量，基于质量守恒、动量守恒、热力学第一及第二定律以及理想气体状态方程，为现代数值天气预报奠定了基础。随着计算能力的提升和观测技术的进步，数值天气预报的准确性和应用范围不断扩大。