参考资料

从代数性质来看，两个向量的外积（叉积）满足分配律，包括左分配律和右分配律。具体来说：

1. 左分配律：对于任意向量 (\mathbf{a})、(\mathbf{b}) 和 (\mathbf{c})，有 (\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c})。这意味着一个向量与另外两个向量和的外积等于该向量分别与这两个向量的外积之和。

2. 右分配律：对于任意向量 (\mathbf{a})、(\mathbf{b}) 和 (\mathbf{c})，有 ((\mathbf{a} + \mathbf{b}) \times \mathbf{c} = \mathbf{a} \times \mathbf{c} + \mathbf{b} \times \mathbf{c})。这意味着两个向量和与一个向量的外积等于每个向量与该向量的外积之和。

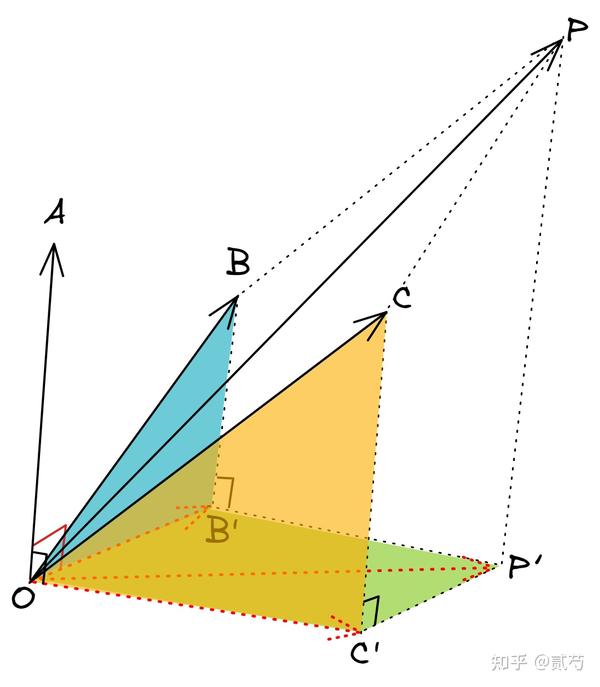
这些分配律可以通过几何方法或代数方法证明。几何证明通常涉及向量构成的平行四边形或平行六面体的面积或体积，而代数证明则依赖于向量分量的运算和行列式的性质。例如，在三维空间中，两个向量 (\mathbf{a} = (a_1, a_2, a_3)) 和 (\mathbf{b} = (b_1, b_2, b_3)) 的外积可以表示为一个行列式： [ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \end{vmatrix} ] 其中 (\mathbf{i})、(\mathbf{j}) 和 (\mathbf{k}) 分别是 (x)、(y) 和 (z) 方向上的单位向量。通过展开这个行列式，我们可以得到外积的分量表达式，进而证明分配律。