细致平衡条件在统计物理中的意义是什么?
参考资料


Moonshot回答
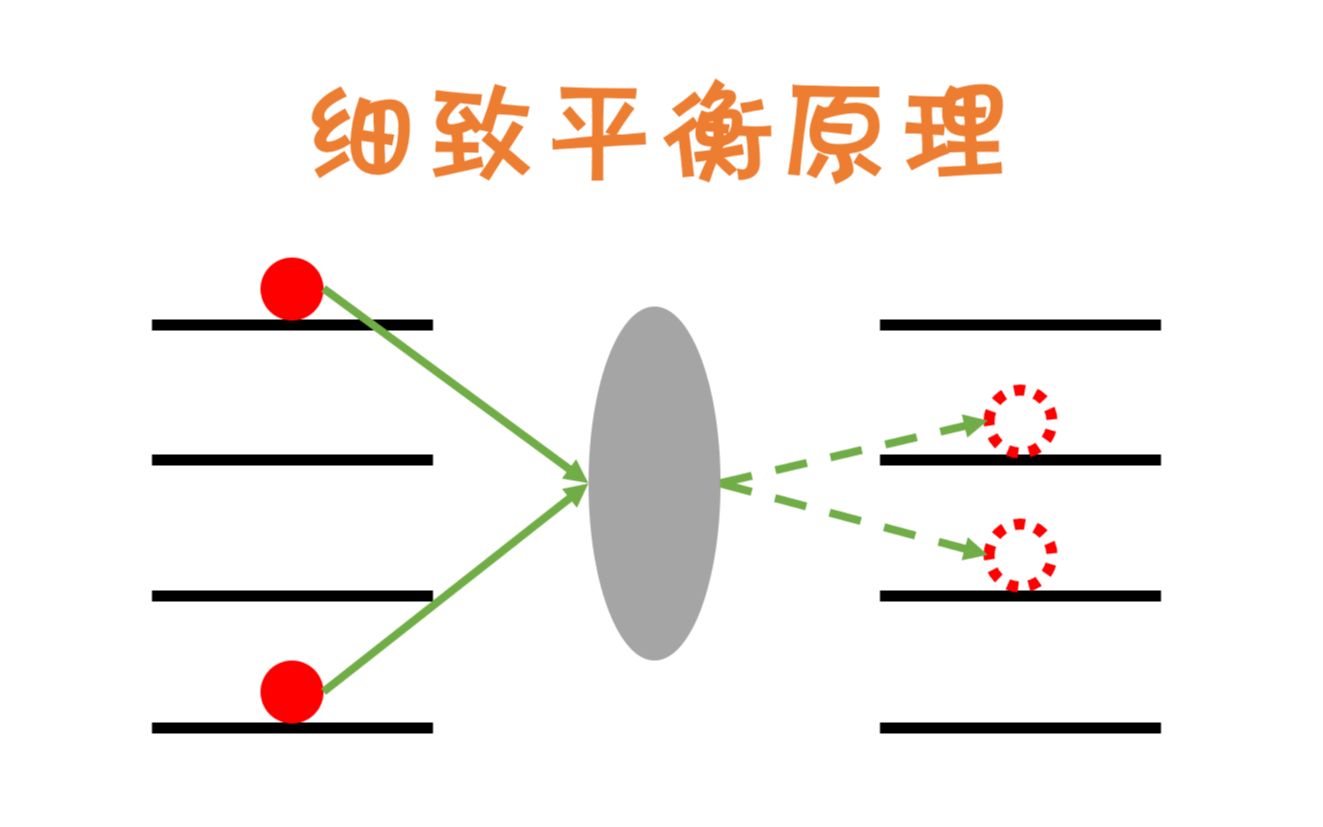
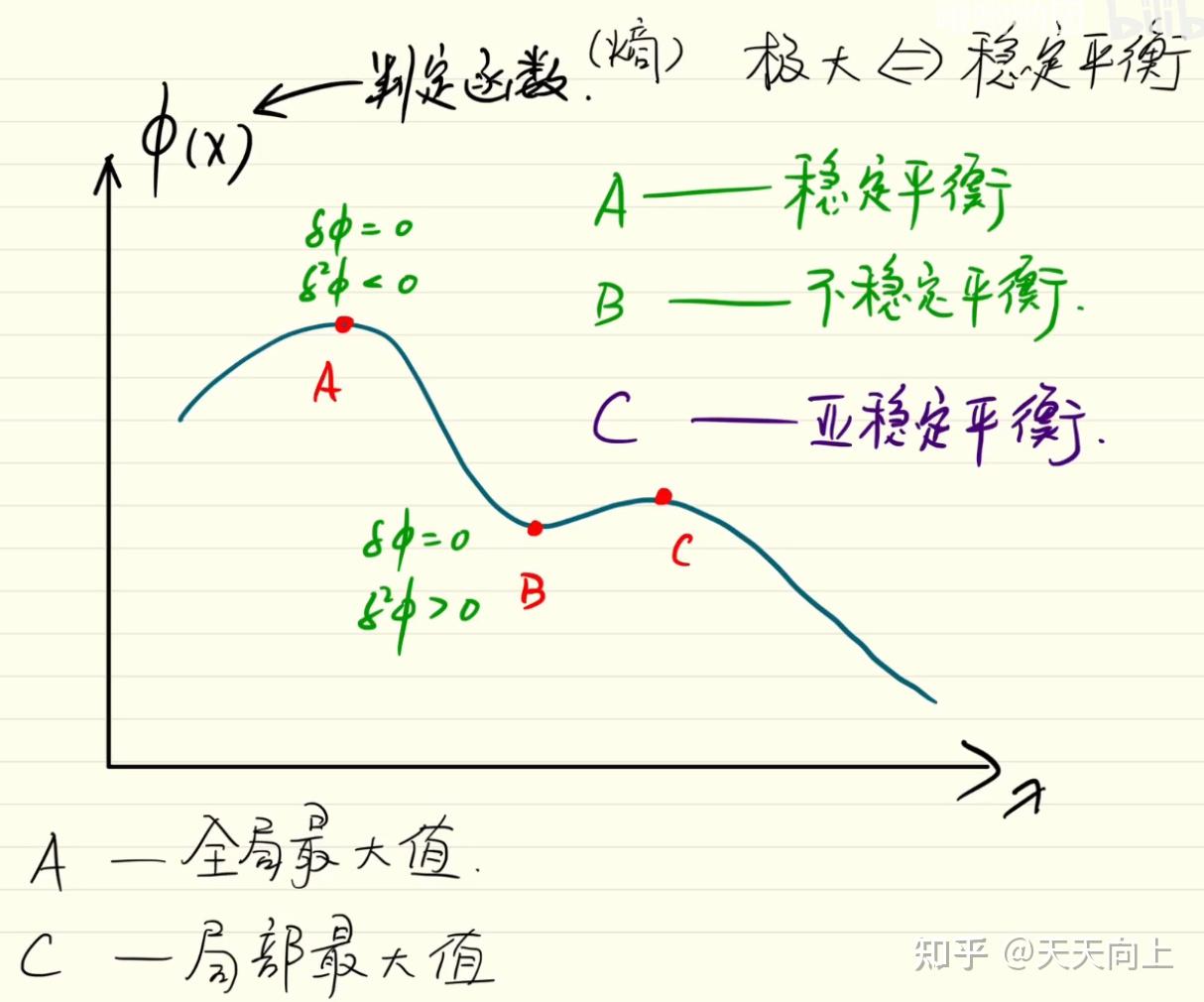
细致平衡条件在统计物理中的意义是多方面的。它关系到一个随机过程的可逆性,与动力学过程、信息的熵产生、生成元和转移半群的谱性质都有重要的联系。在非平衡统计物理中,很多结论都依赖于细致平衡条件等价得到的可逆性结论来证明。此外,细致平衡条件也与马尔科夫链的平稳分布有关,它是一个充分条件,表明如果一个马尔科夫链满足细致平衡条件,那么它具有一个平稳分布。然而,这并不是必要条件,意味着存在不满足细致平衡条件但具有平稳分布的马尔科夫链。在蒙特卡洛模拟中,细致平衡条件确保了模拟得到的分布与目标分布相同,这是通过模拟过程中的转移概率来实现的。总的来说,细致平衡条件是统计物理中一个基础且重要的概念,它在理解和模拟物理系统的行为中起着核心作用。
继续提问
相关问题
为什么通过识别市场传事的阶段可以帮助投资者进行更好的投资决策?
在电影《九人禁闭室》中,这个故事的主要情节是什么?
英格蘭遺產委員會管理的歷史建築中,哪些是亨利八世時期建造的城堡?
卡利什和平条约中,波兰国王卡齐米日三世为何放弃对波美拉尼亚的所有权,却没有实际将土地交给条顿骑士团?
斯威士兰的芦苇节传统上并非为选妃而设,为什么国王却常在此节日中选妃?
美元指数回落和中美利差倒挂加深会对全球市场的资本流动和投资选择产生什么影响?
不同类型的干涉仪有哪些,分别有什么特点和用途?
权赫秀在 'SNL Korea' 中是以什么身份出现的,他在节目中有何表现?
电影《龙与雀斑公主》的IMAX版本是如何呈现出特别的视觉效果的?
德国在1990年统一后,如何在国际组织中保持其成员资格?