能量最小化在分子力学中的应用是什么,哪些算法通常用于找到分子的局部最小能量点?
参考资料
参考资料

Moonshot回答
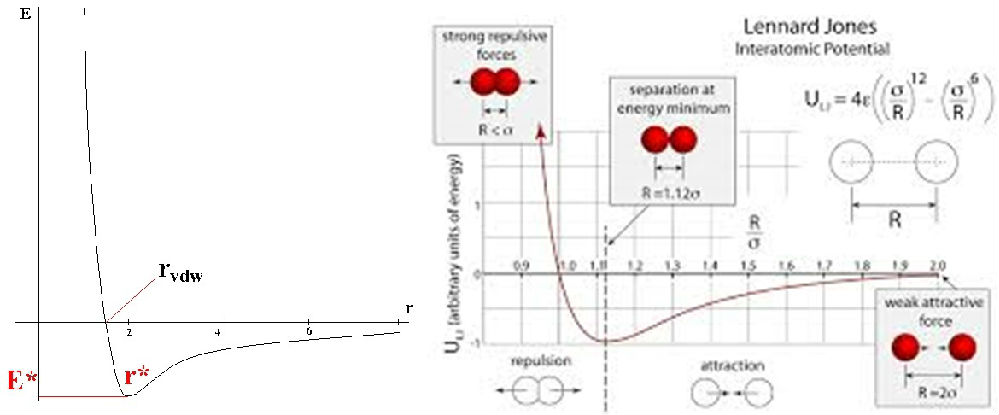
能量最小化在分子力学中是一个关键步骤,它用于寻找分子系统的稳定构象,即局部最小能量点。这个过程有助于消除分子模型中的不合理构象,比如不自然的键角和键长,从而为进一步的分子动力学模拟或自由能计算提供合适的起点。
通常用于找到分子局部最小能量点的算法包括:
-
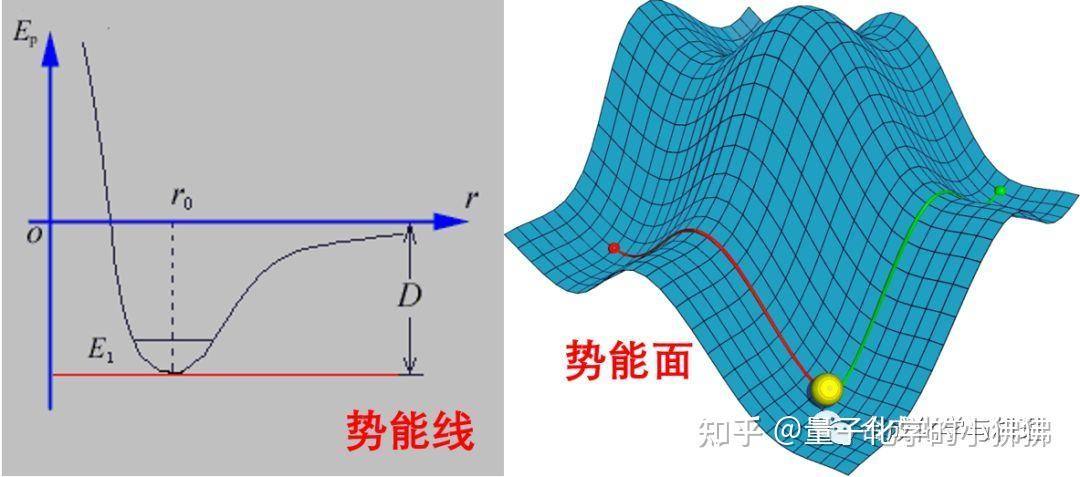
最陡下降法(Steepest Descent, SD):这是一种简单直观的方法,通过势能函数的负梯度方向(即最陡下降方向)迭代寻找能量最小点。虽然计算速度快,但可能在接近最小值时收敛缓慢。
-
共轭梯度法(Conjugate Gradient, CG):这种方法利用了势能函数的Hessian矩阵(二阶导数)信息,通过构建一组共轭方向来加速收敛。它比最陡下降法更有效,尤其是当初始猜测远离真实最小值时。
-
牛顿-拉弗森法(Newton-Raphson, NR):此方法使用Hessian矩阵和梯度信息来寻找最小值。它通常比前两种方法收敛更快,但需要计算和存储Hessian矩阵,计算成本较高。
-
拟牛顿法(Quasi-Newton):这是一种近似牛顿法的方法,不需要显式计算Hessian矩阵,而是通过迭代过程中的梯度信息来近似它。
-
Levenberg-Marquardt算法:这是一种结合了最陡下降法和高斯-牛顿法的算法,通过引入一个调整参数来平衡两者,从而在不同阶段优化收敛速度和方向。
在实际应用中,能量最小化算法的选择取决于分子系统的复杂性、初始猜测的准确性以及计算资源的可用性。有时,为了提高效率和准确性,会结合使用多种算法,例如先使用最陡下降法快速接近最小值,然后切换到共轭梯度法进行精细优化。
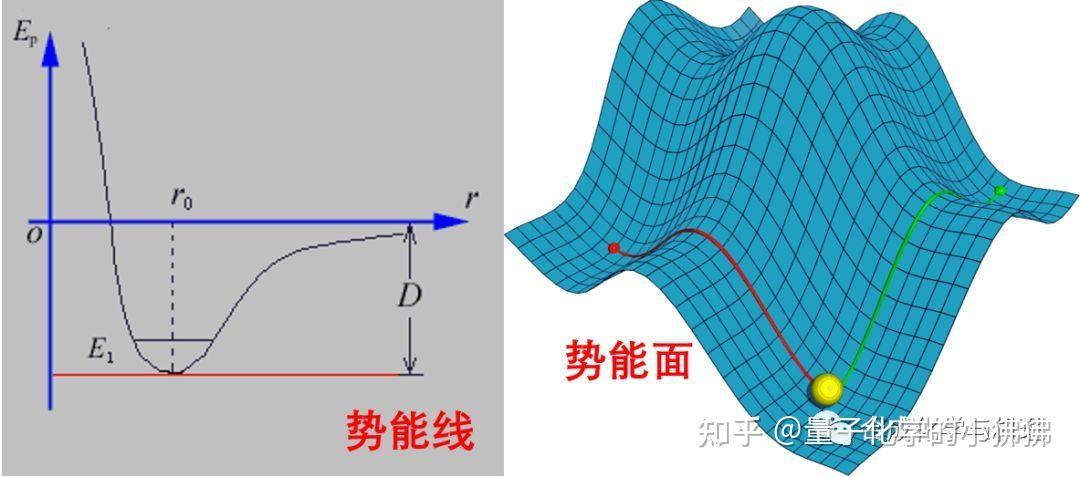
图片来源:知乎专栏,展示了能量最小化过程中能量变化的趋势。