在一维易辛模型中,相邻自旋的相关函数如何定义和计算?
参考资料


Moonshot回答
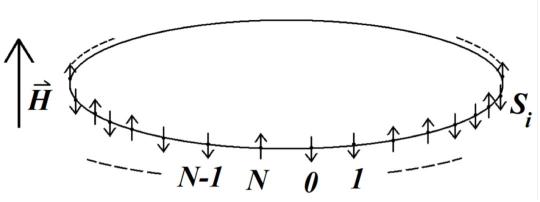
在一维易辛模型中,相邻自旋的相关函数定义为两个相邻自旋的乘积的期望值。具体来说,对于一维晶格上的自旋系统,相邻自旋的相关函数可以表示为:
[ \langle s_i s_{i+1} \rangle ]
其中 ( s_i ) 和 ( s_{i+1} ) 分别代表第 ( i ) 个和第 ( i+1 ) 个自旋的自旋状态,其值可以是 +1 或 -1,分别代表自旋向上或向下。相关函数的计算通常需要考虑系统的哈密顿量,对于一维易辛模型,哈密顿量可以表示为:
[ H = -J \sum_{\langle i,j \rangle} s_i s_j - h \sum_{i=1}^N s_i ]
其中 ( J ) 是相邻自旋之间的交换作用常数,( h ) 是外部磁场,求和 ( \sum_{\langle i,j \rangle} ) 仅对相邻自旋进行。
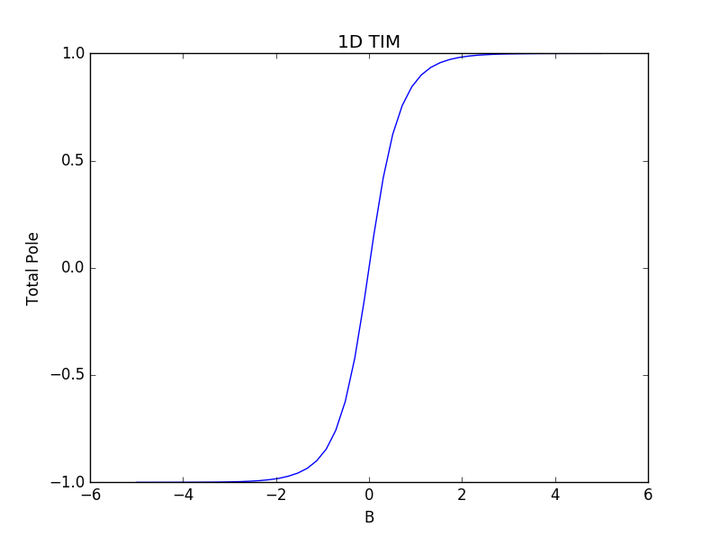
在计算相关函数时,可以通过统计物理方法,如蒙特卡洛模拟或解析方法(例如对于一维无周期性边界条件的情况)来计算。相关函数的计算结果可以反映系统内部自旋的排列方式,例如在铁磁相中,相邻自旋倾向于同向排列,相关函数为正;而在反铁磁相中,相邻自旋倾向于反向排列,相关函数为负。
从搜索结果中,我们可以看到一维易辛模型的相关函数可以通过不同的方法来计算,包括使用平均场理论、蒙特卡洛模拟等。相关函数的计算对于理解系统的磁性行为和相变非常重要。例如,通过计算相关函数,我们可以了解系统在不同温度和磁场下的行为,以及系统如何从铁磁相转变为顺磁相。