薛定谔方程如何用波函数计算粒子在特定位置出现的概率?
参考资料
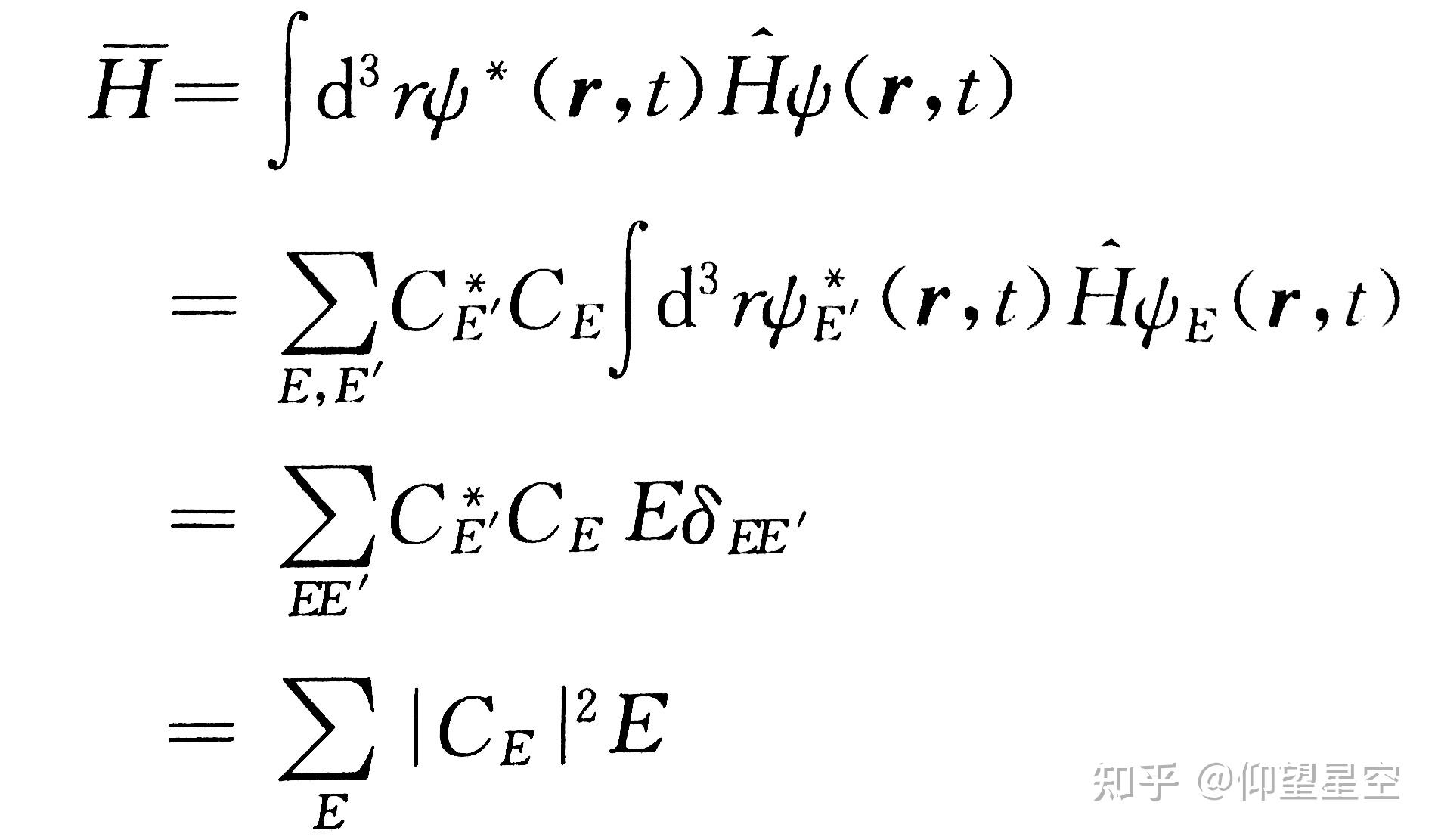

Moonshot回答
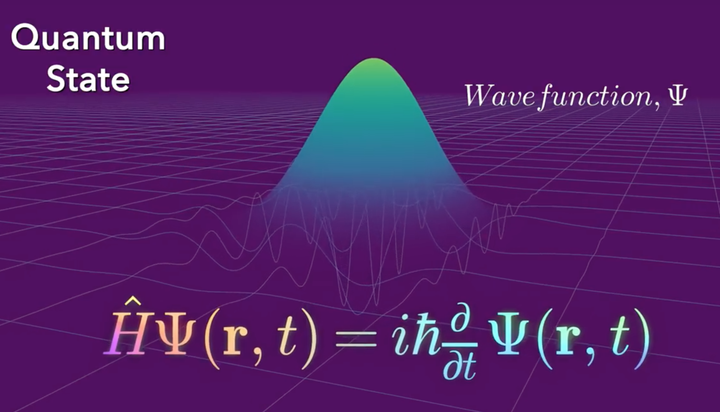
薛定谔方程是量子力学中描述微观粒子状态随时间变化的基本方程。它由奥地利物理学家埃尔温·薛定谔在1926年提出。该方程的波函数 (\Psi(\boldsymbol{r}, t)) 表示粒子在位置 (\boldsymbol{r}) 和时间 (t) 的量子态。波函数的绝对值的平方 (|\Psi(\boldsymbol{r}, t)|^2) 被解释为粒子在该位置出现的概率密度。
具体来说,要计算粒子在特定位置出现的概率,需要先解薛定谔方程得到对应量子态的波函数 (\Psi(\boldsymbol{r}, t))。然后,通过计算波函数在该位置的绝对值的平方,即 (|\Psi(\boldsymbol{r}, t)|^2),就可以得到粒子在这一位置出现的概率密度。对这一概率密度在空间进行积分,就可以得到粒子出现在特定区域的概率。
例如,氢原子的电子在空间中某点出现的概率密度可以通过求解氢原子的薛定谔方程得到。氢原子的波函数通常用量子数 (n)、(l) 和 (m) 来标记,分别对应主量子数、角量子数和磁量子数。通过求解薛定谔方程,可以得到描述电子在不同能级和轨道上的波函数,进而计算出电子在空间中某点出现的概率密度。
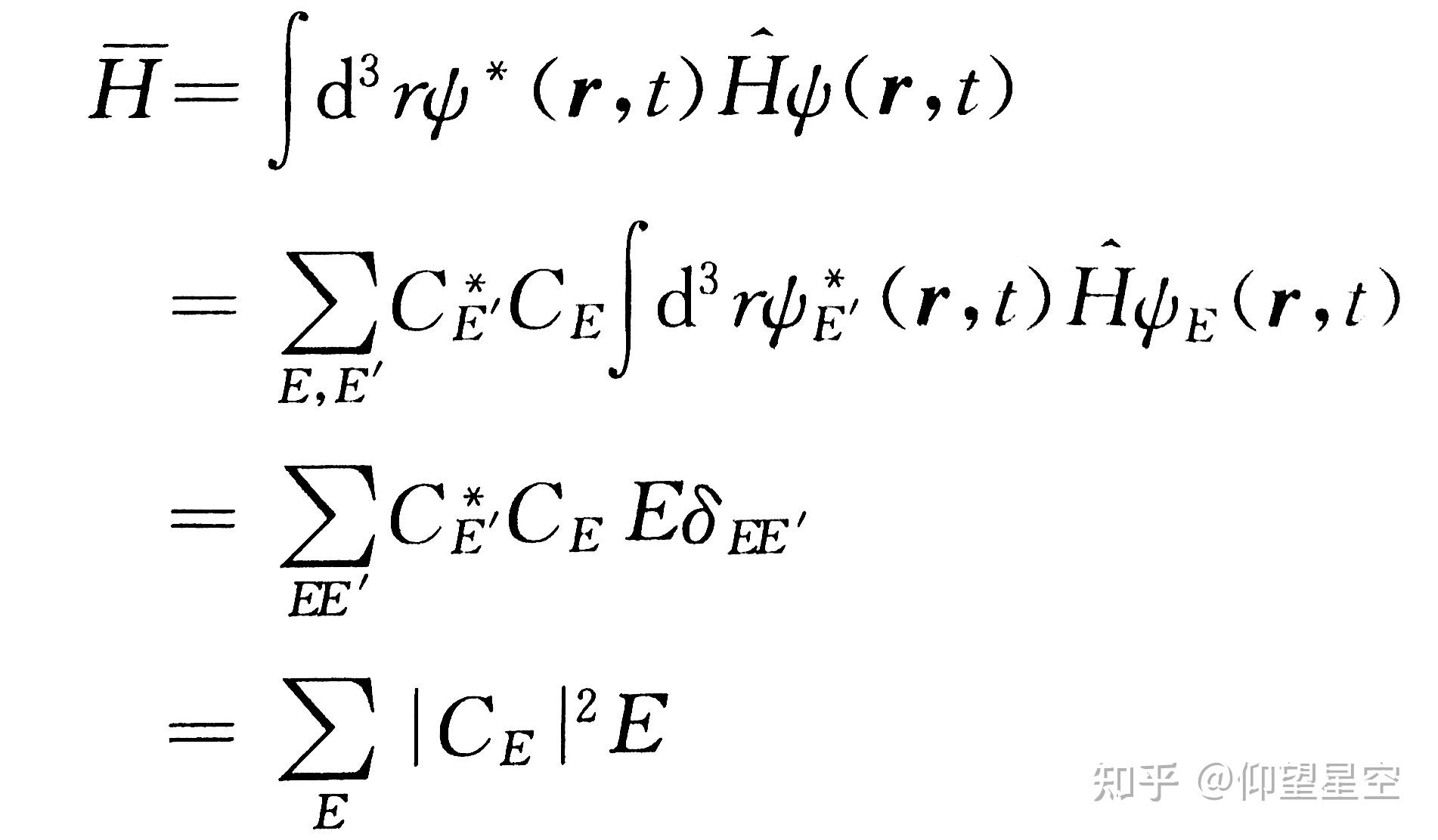
这张图片展示了氢原子电子云的分布,其中颜色的深浅表示电子在不同区域出现概率的高低。通过薛定谔方程计算得到的波函数,可以直观地展示出电子在原子空间中的概率分布情况。来源