参考资料
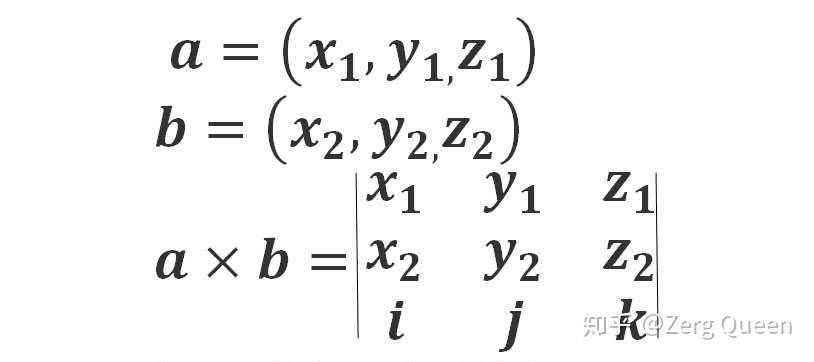
Moonshot回答
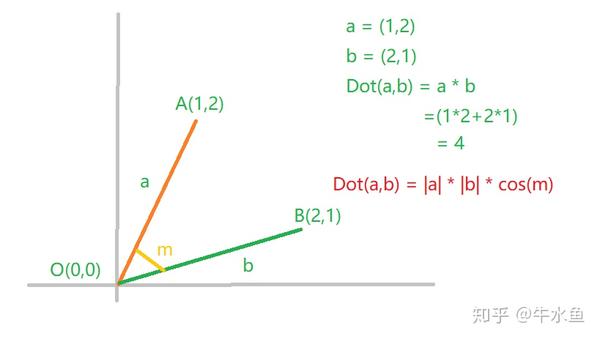
通过基向量计算两个向量的叉积,具体步骤如下:
-
确定向量的分量:设两个向量分别为 (\mathbf{a} = (a_1, a_2, a_3)) 和 (\mathbf{b} = (b_1, b_2, b_3))。
-
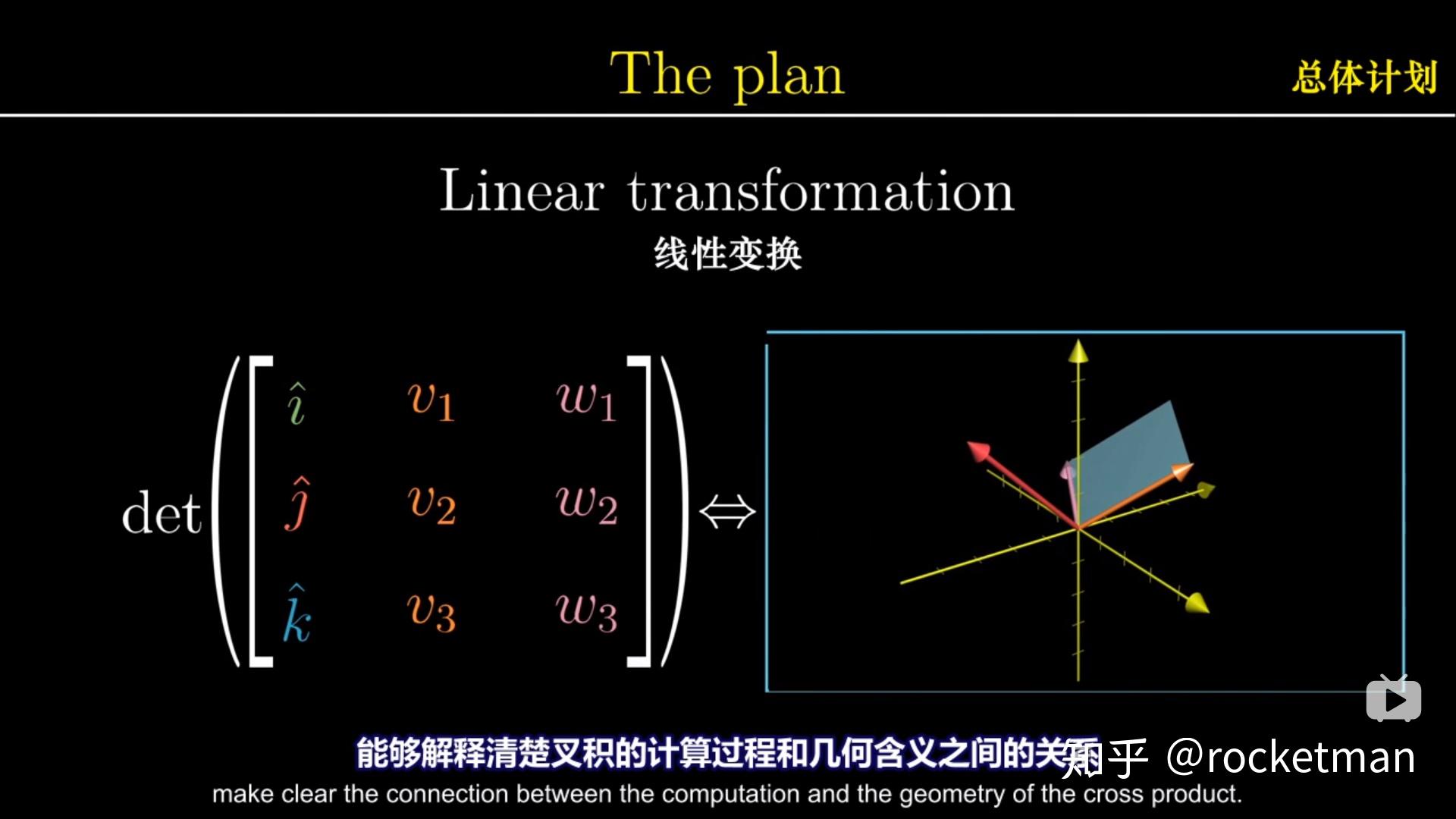
使用行列式公式计算叉积:叉积 (\mathbf{a} \times \mathbf{b}) 可以通过以下行列式来计算: [ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \end{vmatrix} ] 其中,(\mathbf{i}),(\mathbf{j}),和 (\mathbf{k}) 分别是 (x),(y),和 (z) 方向上的单位向量。
-
展开行列式:计算行列式得到叉积的各个分量: [ \mathbf{a} \times \mathbf{b} = (a_2b_3 - a_3b_2)\mathbf{i} - (a_1b_3 - a_3b_1)\mathbf{j} + (a_1b_2 - a_2b_1)\mathbf{k} ]
-
应用结果:得到的向量 (\mathbf{a} \times \mathbf{b}) 垂直于 (\mathbf{a}) 和 (\mathbf{b}),其方向由右手定则确定,其大小等于以 (\mathbf{a}) 和 (\mathbf{b}) 为邻边的平行四边形的面积。
-
验证和应用:叉积在物理学中,特别是在计算力矩和角动量时非常重要。它也可以用于确定两个向量是否平行,或者计算两个向量之间的夹角。
通过以上步骤,你可以计算出任意两个三维空间向量的叉积。如何用叉乘算法向量 | PingCode智库 提供了详细的步骤说明。此外,叉积的几何意义及应用在 向量叉积(Cross product)的几何意义及应用 - CSDN博客 中有更深入的探讨。