什么是量子纠缠,为什么它在量子力学中如此重要?
参考资料



参考资料


Moonshot回答
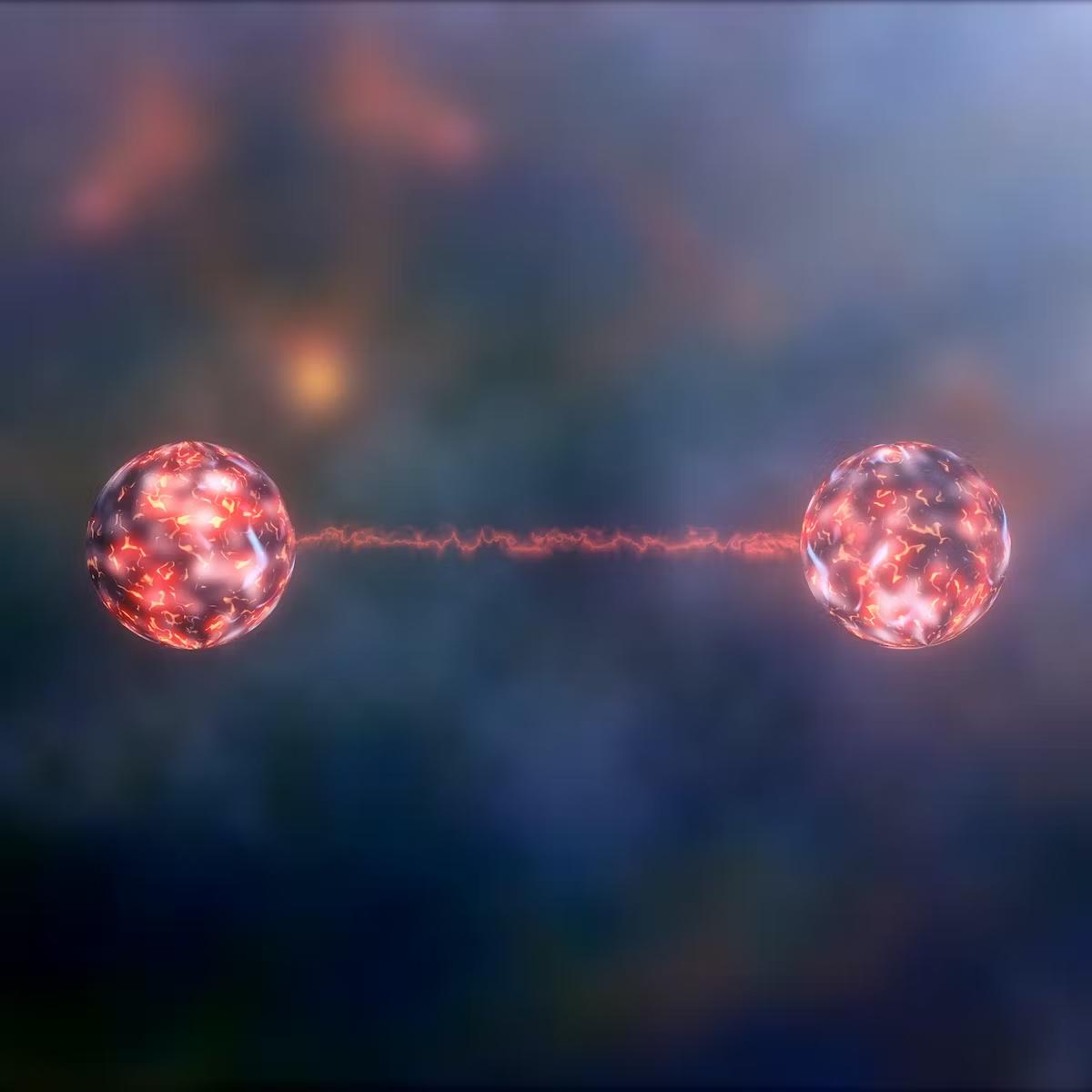
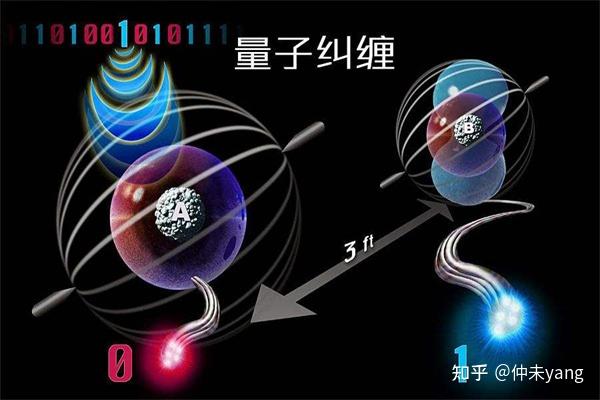
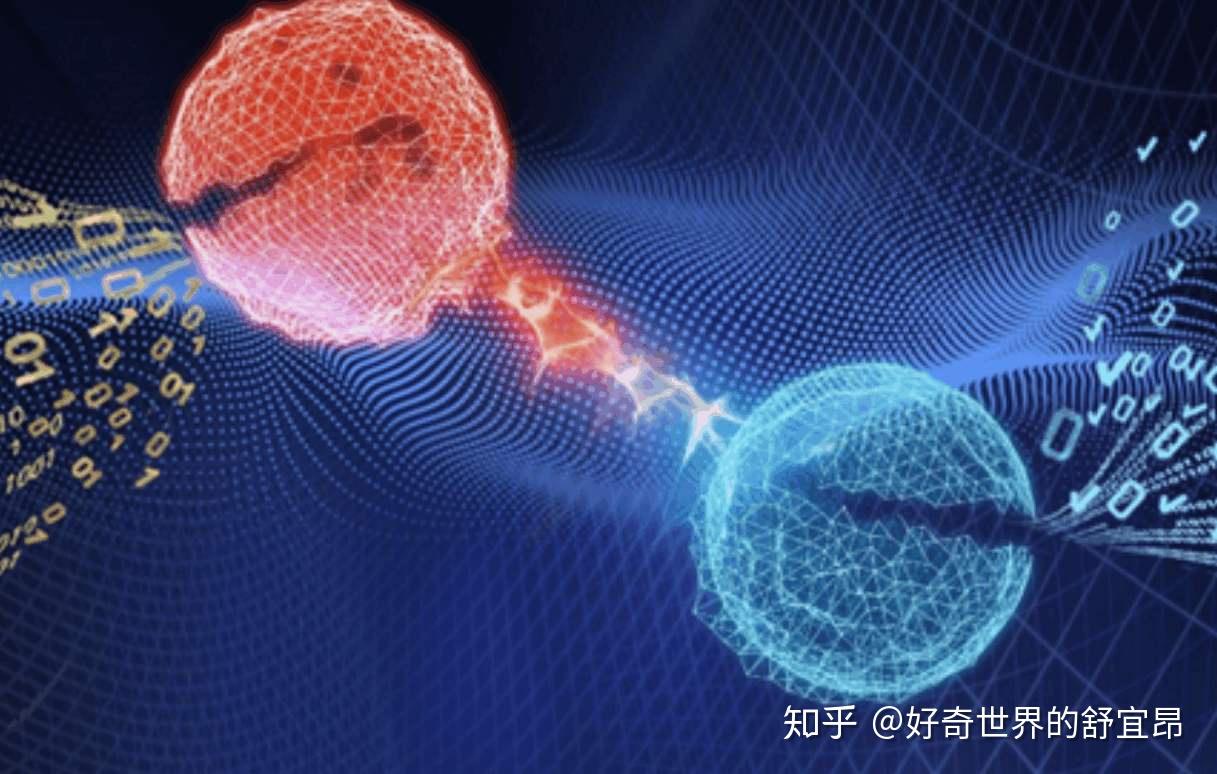
量子纠缠是量子力学中一种非常奇特的现象,其中两个或多个粒子相互链接到其中一个粒子的状态无论其距离多远,都能立即影响另一个粒子的状态。这种纠缠状态下的粒子共享量子状态,而量子状态的描述无法单独对每个粒子进行,只能对整个系统进行。
量子纠缠的重要性在于它不仅展示了量子世界与我们日常经验的差异,而且在量子信息科学领域,包括量子计算、量子通信和量子密钥分发等方面,都有极其重要的应用。例如,量子纠缠可以用于实现量子隐形传态,这在理论上允许信息在没有实际传输载体的情况下瞬时“传送”。此外,量子纠缠还在量子计算机的开发中扮演着关键角色,因为量子计算机利用量子纠缠来进行高效的并行计算,解决某些对于传统计算机来说几乎不可能解决的问题。
量子纠缠的这些特性和潜在应用前景,使其成为了量子力学和量子信息科学中最活跃的研究领域之一。随着量子技术的发展,我们有望实现更稳定、更高效的量子纠缠态的储存和保护方法,进一步拓展量子通信和量子计算的应用领域。量子互联网的构建和量子网络的发展也将成为重要研究方向,为我们带来更加高效和安全的信息传输和通信方式。
 图片来源:知乎
图片来源:知乎
以上信息整合了来自网络搜索的结果,包括对量子纠缠的定义、特性、以及它在量子力学和量子信息科学中的重要性的解释。