参考资料

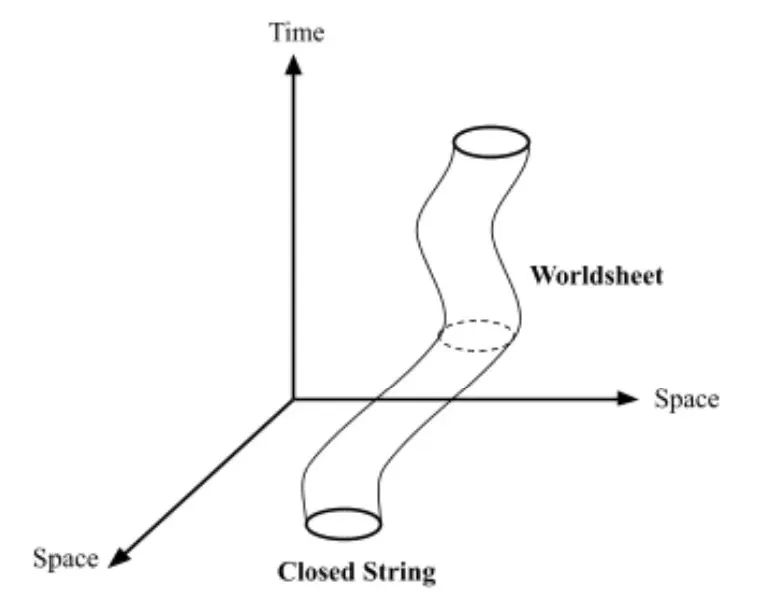
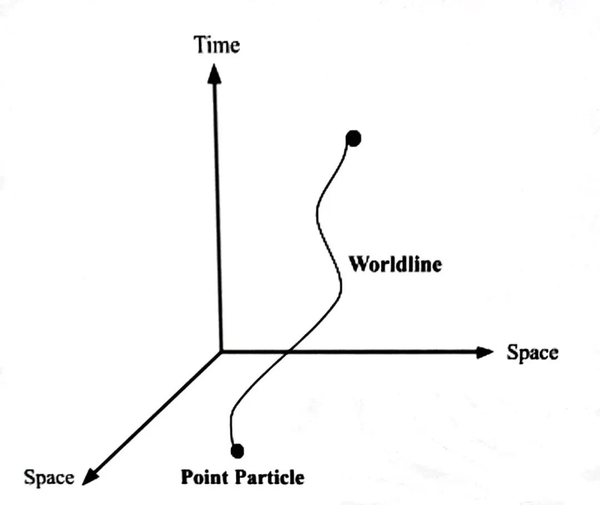
弦理论中的世界面是一个二维流形，用于描述弦在时空中的嵌入情况。这个概念由伦纳德·萨斯坎德在1967年左右提出，是点粒子世界线概念的推广。在弦理论中，世界面的作用非常关键，它不仅编码了弦的类型和它所传播的时空的几何形状，还包含了远距离背景场论（如规范场论）的信息。

世界面在弦理论中的作用主要体现在以下几个方面：

1. 描述弦的动力学：世界面通过函数 ( X^{\mu}(\sigma, \tau) ) 描述弦在时空中的嵌入，其中 ( \sigma ) 和 ( \tau ) 是世界面上的坐标。
2. 弦的相互作用：在弦理论中，相互作用可以被理解为世界面拓扑的结果，而不是世界面上的局域奇点。例如，开弦的端点可以附着在其他对象上，如D膜，而闭弦则可以自我相互作用。
3. 量子引力的框架：弦理论提供了一个完全一致的框架来统一所有相互作用，包括量子引力。世界面在这一框架中扮演了基础的角色，使得引力可以以量子化的方式与其他基本力统一。
4. 黑洞物理：研究弦理论中的黑洞，特别是极端黑洞的世界面，也导致了黑洞与纯数学之间的许多联系的发现。

此外，世界面的概念也与弦理论中的微扰展开有关，其中涉及各种拓扑结构的弦世界面。这些世界面的不同拓扑结构对应于不同的物理过程，如弦的分裂和合并。

总的来说，世界面在弦理论中扮演着基础且核心的角色，它不仅是描述弦动力学的舞台，也是理解和统一所有基本相互作用的关键。