什么是Hessian矩阵,它在多维牛顿法中的作用是什么?
参考资料
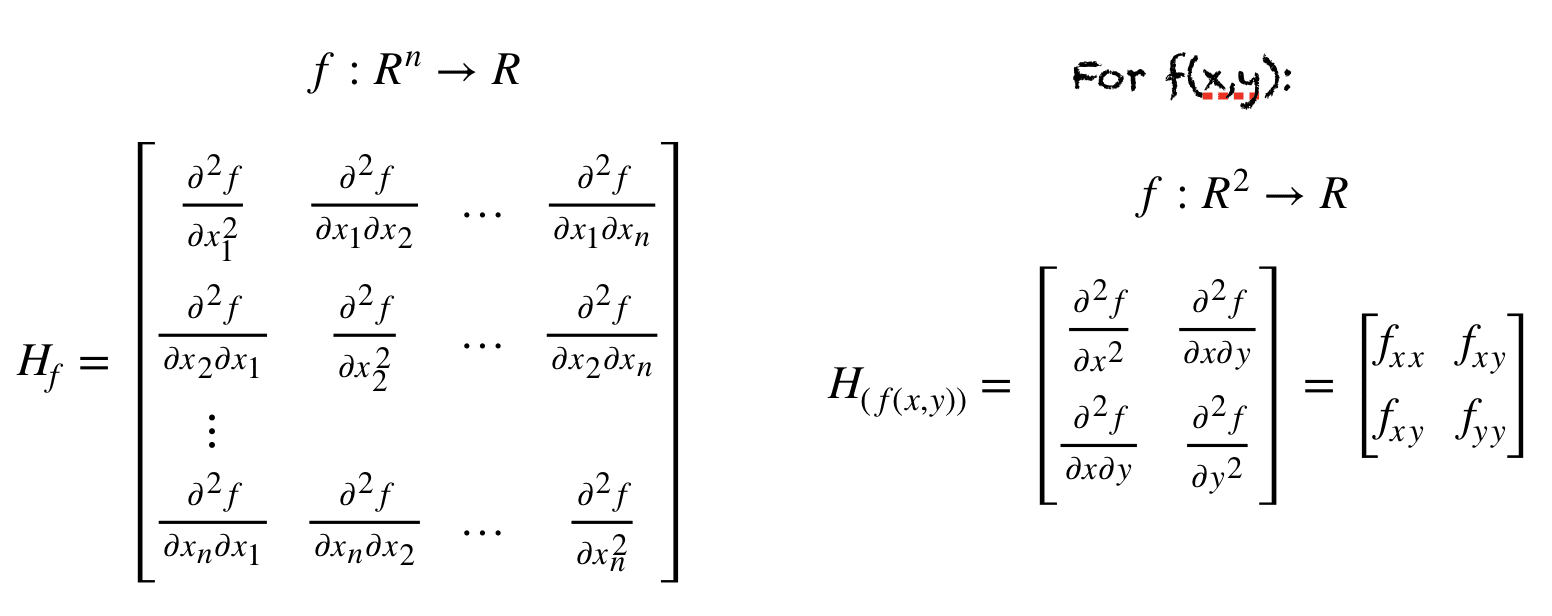



Moonshot回答
Hessian矩阵是多元函数的二阶偏导数构成的方阵,它在多维牛顿法中扮演着至关重要的角色。多维牛顿法利用Hessian矩阵来确定搜索最优解时的步长和方向,以实现快速收敛。具体来说,Hessian矩阵提供了目标函数曲率的信息,帮助决定在每一步迭代中如何调整参数以更接近最小值。
然而,Hessian矩阵的使用也带来了一些挑战。首先,Hessian矩阵必须正定才能保证算法的收敛,但在非凸问题中,Hessian矩阵可能非正定,导致算法无法收敛。其次,随着问题维度的增加,Hessian矩阵的计算和存储需求急剧增加,这可能导致计算复杂度和资源消耗过大。
为了解决这些问题,研究者们提出了多种改进方法,如拟牛顿法,它通过近似Hessian矩阵来降低计算成本,同时保持较快的收敛速度。此外,还有一些方法专注于保持Hessian矩阵的正定性,以确保算法的稳定性和收敛性。
以下是一些与Hessian矩阵和多维牛顿法相关的图像资源:
这些资源可以帮助更直观地理解Hessian矩阵在多维优化问题中的应用和影响。