玻尔兹曼常数在配分函数的计算中起到什么作用?
参考资料
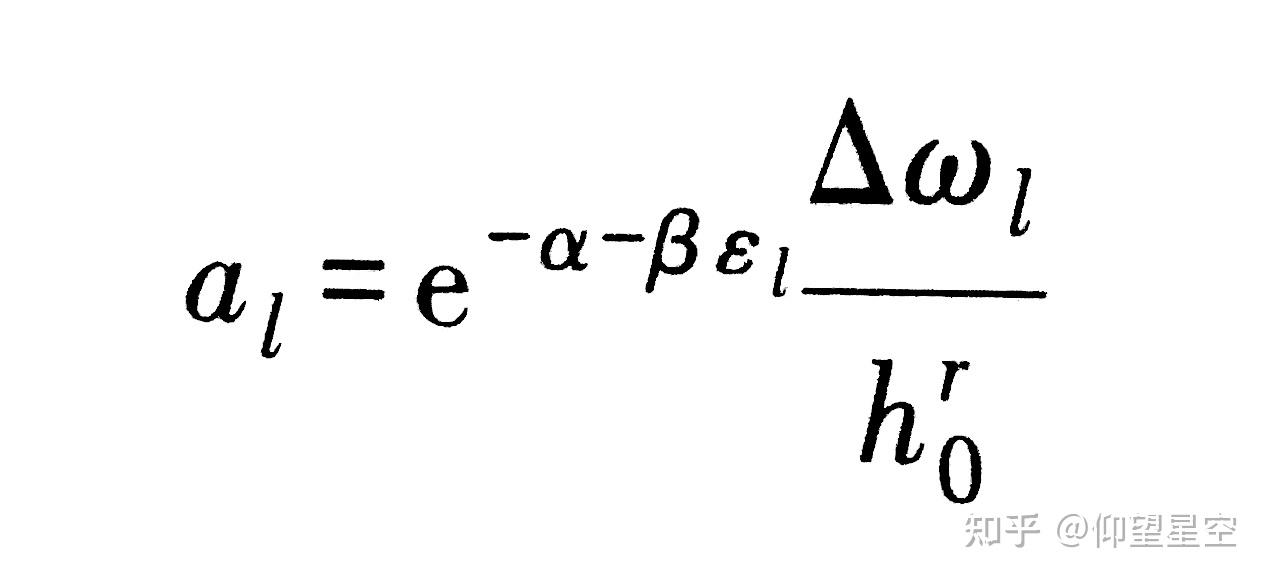
Moonshot回答
玻尔兹曼常数((k_B))在配分函数的计算中扮演着至关重要的角色。配分函数是统计物理学中一个核心概念,它将系统的微观状态与宏观物理量联系起来。配分函数通常定义为系统所有可能微观状态的求和,每个状态乘以其相应的玻尔兹曼因子 (e^{-\frac{E}{k_B T}}),其中 (E) 是状态的能量,(T) 是温度。
配分函数的数学表达式为: [ Z = \sum_i \omega_i e^{-\frac{E_i}{k_B T}} ] 其中,(\omega_i) 是第 (i) 个能级的简并度,(E_i) 是该能级的能量。
玻尔兹曼常数确保了配分函数的量纲正确,并且使得配分函数与温度相关。它允许配分函数在不同温度下正确地计算系统的概率分布。此外,配分函数的对数与亥姆霍兹自由能相关,这使得我们能够从配分函数导出系统的内能、熵、焓等热力学量。
通过搜索结果,我们可以看到配分函数在统计物理学中的应用非常广泛,它与玻尔兹曼常数紧密相关,用于计算系统的宏观物理量。例如,从配分函数可以计算出系统的内能、熵和物态方程等。玻尔兹曼常数在这些计算中起到了桥梁的作用,将微观状态的能量与宏观物理量联系起来。