周期性边界条件在模拟物理系统过程中起什么作用?
参考资料
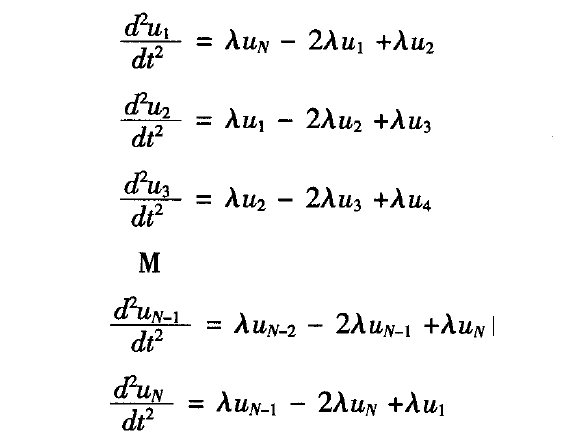
Moonshot回答
周期性边界条件在模拟物理系统过程中扮演着重要角色。它通过将一个有限的计算区域扩展为一个周期性的、重复的单元,来近似表示无限或半无限的物理系统。这种条件在数学建模和计算机仿真中非常常见,特别是在分子动力学模拟、固体物理、光学波导和电磁学等领域。
周期性边界条件的主要作用包括:
- 模拟无限或半无限系统:通过周期性复制有限的计算区域,可以模拟更大尺度的物理现象。
- 减少边界效应:周期性边界条件可以减少边界对系统的影响,使模拟结果更加准确。
- 保持系统的连续性和对称性:在某些情况下,周期性边界条件可以保持系统的连续性和对称性,这对于某些物理量的计算非常重要。
例如,在分子动力学模拟中,周期性边界条件通常用于计算散装气体、液体、晶体或混合物。此外,周期性边界条件还可以用于模拟具有周期性结构的材料,如晶体和超晶格。
在实际应用中,周期性边界条件有多种类型,包括连续性周期边界、反对称周期边界和弗洛奎特周期性边界等。这些不同类型的周期性边界条件可以根据具体的物理问题和模拟需求来选择。
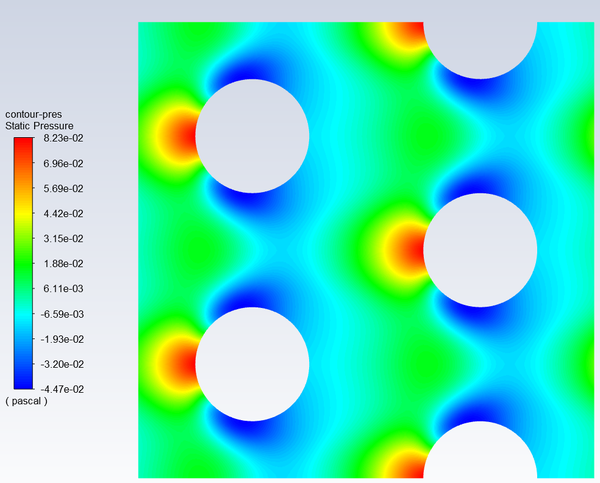
 图片来源:中国仿真互动网
图片来源:中国仿真互动网
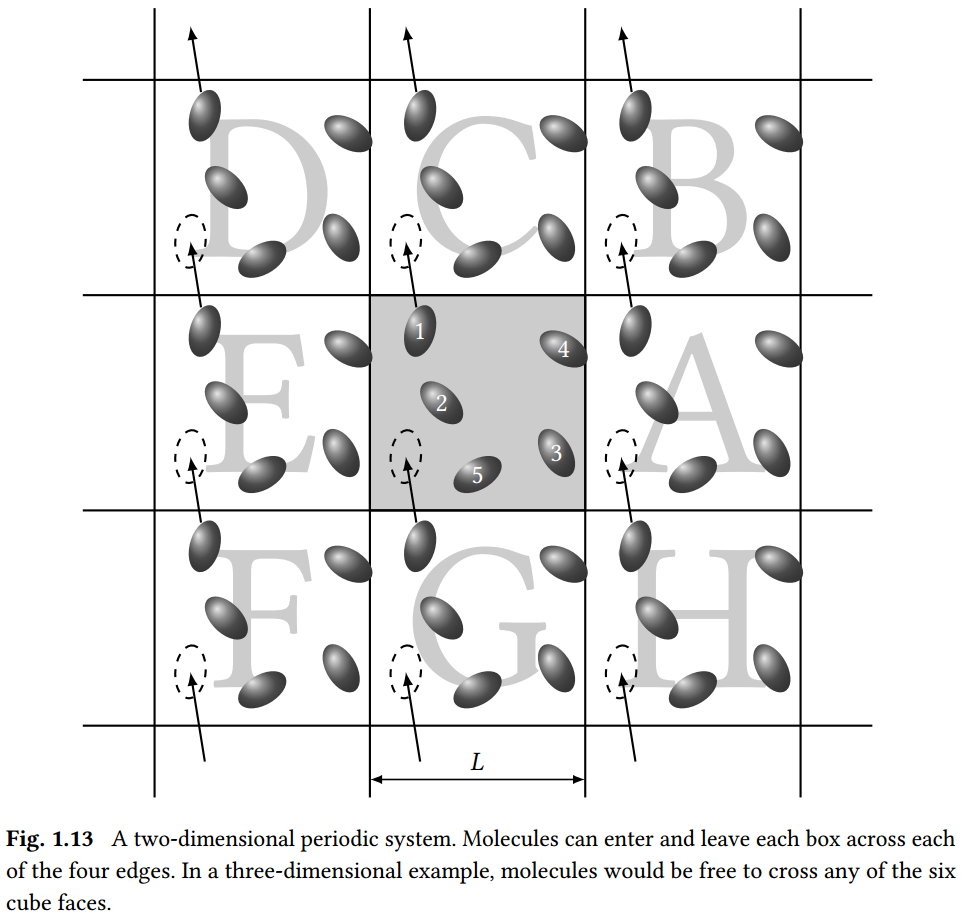
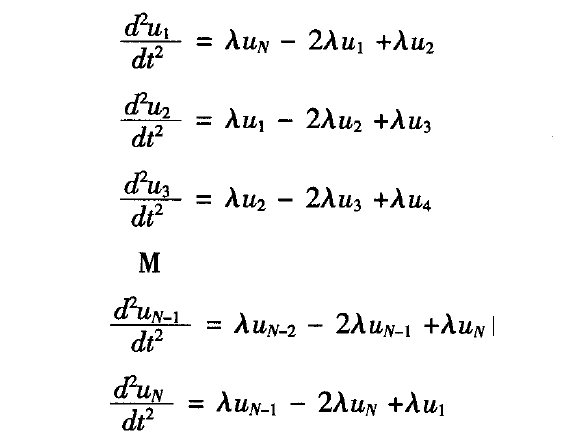 图片来源:维基百科
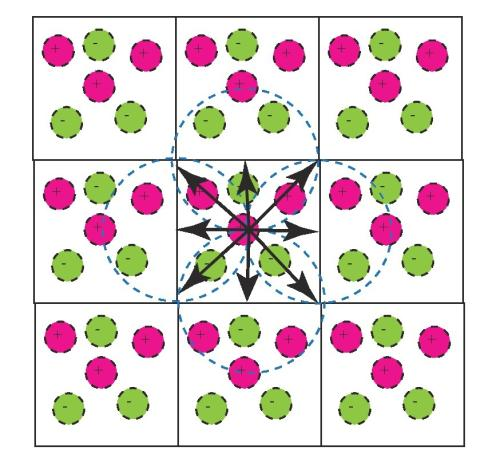
图片来源:维基百科
这些图片展示了周期性边界条件在不同物理系统中的表示,有助于理解其在模拟过程中的作用。