能否解释劳伦兹因子的公式内容及其在相对论中的重要性?
参考资料


参考资料
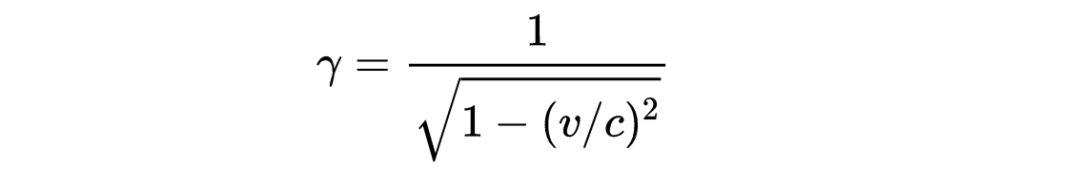
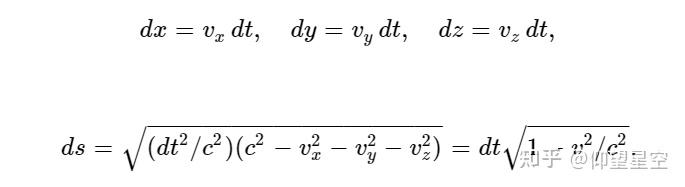
Moonshot回答
劳伦兹因子(Lorentz factor),也称洛伦兹因子或洛伦兹缩放因子,是狭义相对论中一个重要的概念。它描述了在不同惯性参考系之间进行变换时,时间和空间坐标如何变化。劳伦兹因子的公式为:
[ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} ]
其中:
- ( \gamma ) 是劳伦兹因子
- ( v ) 是物体的速度
- ( c ) 是光速
劳伦兹因子在相对论中的重要性体现在以下几个方面:
- 时间膨胀:在高速运动的参考系中,时间会变慢。具体来说,运动参考系中的时间间隔 ( \Delta t' ) 与静止参考系中的时间间隔 ( \Delta t ) 之间的关系为 ( \Delta t' = \gamma \Delta t )。
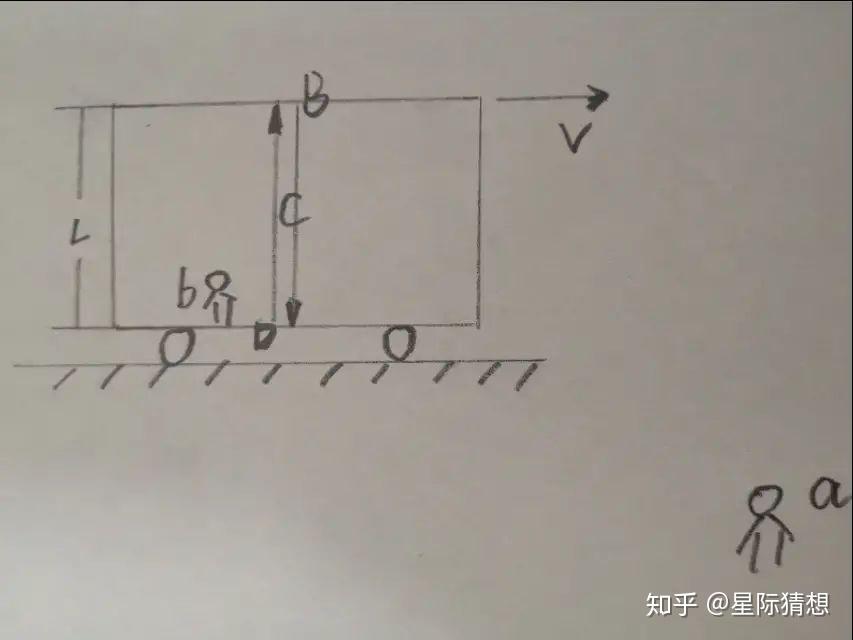
- 长度收缩:在高速运动的参考系中,物体在运动方向上的长度会变短。长度收缩的公式为 ( L' = \frac{L}{\gamma} ),其中 ( L ) 是物体在静止参考系中的长度,( L' ) 是在运动参考系中观察到的长度。
- 相对论质量增加:随着物体速度的增加,其质量也会增加。相对论质量的公式为 ( m' = \gamma m ),其中 ( m ) 是物体的静止质量,( m' ) 是在高速运动时的质量。
劳伦兹因子是理解和计算这些相对论效应的关键。它揭示了在接近光速时,物理现象与经典物理学预测的显著不同。通过劳伦兹因子,我们可以更准确地描述和预测在高速运动中的物理现象。
 图片来源:知乎
图片来源:知乎
 图片来源:人民日报
图片来源:人民日报
这些图片展示了劳伦兹因子与速度的关系,以及在不同速度下劳伦兹因子的值。随着速度接近光速,劳伦兹因子会趋于无穷大,这表明相对论效应变得非常显著。