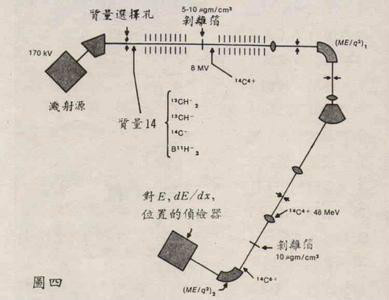
目次 放射性碳定年法 放射性碳定年法[1],亦作放射性碳測年[2]、14C測年方法[2]、放射性14C定年法[3]等,是一種利用碳的同位素14C的放射性來對含有有機物質的物品進行年代測定(英語:Chronological dating)的方法。 威拉得·利比於1940年代在美國芝加哥大學發現了放射性碳定年法,並因此在1960年獲得諾貝爾化學獎。這種方法基於大氣中的氮與宇宙線反應不斷在大氣中產生放射性碳(14C),這些14C與大氣中的氧結合形成具有放射性的二氧化碳,又透過植物的光合作用進入生物圈,然後再被動物進食攝入體內,故此所有的生物終其一生都不斷地與大自然交換著14C,直至死亡。這個交換在死後會停止,14C的含量就會透過放射衰變逐步減少。透過測量死去動植物樣本的14C含量,例如一塊木頭或者一段骨頭,就可以推算出動植物死亡的時間。樣本越古老,可檢測到的14C含量就越少。因為14C的半衰期(一個樣本的一半衰變的時間週期)大約是5730年,所以這種方法可以可靠地測量所得到的最古老的樣本大約是五萬年左右,不過特殊的製備方法有時可以準確分析更古老的樣本。 1960年代以來,科學家一直在研究過去的五萬年裡大氣中的14C比例,研究結果的數據形成了一條校準曲線,可以透過樣本中放射性碳的測量值來估計樣本的絕對年代。不過,不同類型的生物中14C的含量不同(即同位素分餾),加之環境因素亦會影響生物圈中14C的含量(即碳庫效應),因此計算時必須要進行額外的校準。化石燃料(如煤和石油)的燃燒和50、60年代在近地的核試驗使事情變得更複雜。因為生物體變成化石燃料所需要的時間遠遠比其14C含量降低到可檢測值以下所需的時間要長,因此化石燃料幾乎沒有14C,結果就是自19世紀末期開始,大氣中的14C比例大幅下降。反過來,核試驗大大提高了大氣中14C的含量,在1960年代中期達到了最大值,是核試驗之前含量的兩倍。 放射性碳的測量最早使用β粒子計數器,計算樣本中14C原子衰變時放射出的β粒子。而現在人們一般使用加速器質譜法,這個方法能統計樣本中全部的14C原子數量,而不是只統計少量在測量時發生衰變的14C,所以這種方法可以應用在更小的樣本上(如植物種子),結果出的也更快。放射性碳定年法的發展對考古學有著深遠的影響——相較之前的方法,除了可以更準確地給考古遺址斷代,還可以比較距離很遠的地方的兩個事件的發生時間。考古學史上常稱之為「放射性碳革命」。地質學上,放射性碳定年法可以確定史前時代大事件的年份(如末次冰期的結束時間)。 背景 歷史 1939年,勞倫斯伯克利國家實驗室的馬丁·卡門(英語:Martin Kamen)和塞繆爾·魯本(英語:Samuel Ruben)開始進行實驗,以確定是否有機物中常見的任何元素都具有半衰期足夠長的同位素,從而在生物醫學研究中有價值。他們用實驗室的迴旋加速器合成了14C,很快便發現這種原子的半衰期比之前設想的長的多。[4]之後,在費城富蘭克林研究所供職的塞爾日·科爾夫(Serge A. Korff)預測,大氣層上空的14N與熱中子反應會產生14C。[5][6][注 1][注 2]二戰期間,伯克利的威拉得·利比了解到了科爾夫的研究後,產生了可以利用放射性碳來定年的想法。[5][6] 1945年,利比來到芝加哥大學,開始著手進行放射性碳定年法相關的研究。隔年,他在一篇論文中指出,生命體中同時含有14C和非放射性碳。[8][9]他又和其他幾名研究員一道,從巴爾的摩下水道收集了些甲烷並對其進行同位素分離。分析結果表明,這批樣品中含有14C。與此相對的是,那些從石油中收集得到的甲烷因年代久遠根本檢測不到放射性。1947年,這些結果被發表到了《科學》上,文中闡明這意味著人們可以對含碳有機物進行年代檢定。[8][10] 利比隨後與詹姆斯·阿諾德(英語:James R. Arnold)一道,選了一批年代已知的樣品來檢驗放射性碳定年理論。比如,他們從兩位埃及法老左塞爾和斯尼夫魯的墳墓中取樣並測算,歷史學家認為這些樣本年代在公元前2625±75年,而放射性碳測得公元前2800±250年。這些結果在1949年發表到了《科學》上。[11][12][注 3]到了1960年,世界各地已建立了20多所放射性碳定年實驗室。[14]該年,利比為此獲得了諾貝爾化學獎。[8] 物理和化學細節 在自然界中,碳存在兩種穩定且無放射性的同位素,即碳-12(12C)和碳-13(13C),還有一种放射性的同位素碳-14(14C),又被稱為「放射性碳」。14C 的半衰期(給定量的14C中的半數發生衰變所耗費的時間)大約是5,730年,因此如果沒有外部的影響其在大氣中的濃度會在數千年間逐漸減少,但是來自外太空的宇宙射線會在平流層下部和對流層上部不斷產生14C,這些宇宙射線主要來自銀河系,還有少部分是來自太陽。[8][15]宇宙射線會產生中子,當中子撞擊氮-14原子時又產生14C。[8]這個核反應是14C產生的主要途徑: 其中,n表示中子,p表示質子。[16][17][注 4]14C一旦產生就會快速與大氣中的氧氣結合形成一氧化碳(CO)[17],最終形成二氧化碳(CO2)[18]: 透過這種方式產生的二氧化碳擴散至大氣中,溶解在海洋里,然後透過光合作用被植物所吸收,動物再吃掉植物,放射性碳最終會分布到整個生物圈中。14C與12C的比例大約是1.25比1012。[19]另有約1%的碳原子是穩定同位素13C。[8] 14C的放射性衰變方程式為:[20] 透過釋放一個β粒子(即電子,e−)和一個微中子(νe),14C核中的一個中子變成質子,14C的核恢復為穩定的(非放射性)同位素14N。[21] 原理 生物在存活期間會透過呼吸、進食等方式與其周圍的自然環境不斷交換碳元素,並維持一定的平衡。因此,它體內的14C占比與周遭的大氣或海洋的是一致的。生物死亡後會停止攝入14C。然而,在原生物體內的14C會繼續衰變,導致14C/12C比值降低。透過這一比值和已知的14C半衰期得知的14C減少量(樣本越老14C就越少),最後就可以推得此生物的死亡時間。[19]不過,受各種因素影響(見下文),測量出的14C/12C比值通常需要校準後才能得到準確結果。直接用14C/12C比值計算出的結果被稱為「表觀年齡」(apparent age)。[22] 放射性同位素的衰變方程式如下:[8] 其中N0是原始樣本中同位素的原子數量(即時間t = 0處,該生物組織死亡的時刻),N是經過了時間t後樣本中剩餘的原子數量。[8]λ是一個常數,取決於具體的同位素;對於一個給定的同位素,λ等於該同位素原子衰變平均所需時間的期望值(即平均壽命)的倒數。[8]14C的平均壽命是8267年,因此上面的方程式也可以寫作:[23] 人們假設,被測樣本中的14C/12C原始比值應與當時大氣環境中的比值相同。由於樣本質量已知,人們可以透過計算樣本中的原子數量來推出N0(14C原子的數量)。隨後再對當前樣本中14C的原子數量進行測算得到N,再將N0、N代入上文中的公式,即可求得樣本年代t。[19] 相比於平均壽命而言,公眾對於放射性元素「半衰期」(寫作T1/2)的概念更為熟知,因此人們通常引入14C的半衰期作為上文公式中的常量。[注 5]目前普遍認為14C的半衰期是5,730±40年。[8]也就是說,約5730年後,一份樣本中將會只剩下一半14C;過了11460年後則會剩下四分之一;過了17,190年後則只剩下八分之一。 這裡介紹的計算方式以多個假設為前提,只給出了理想狀態下的結果。在實際應用中,14C的含量在各個年代會有較大區別,因此以上方程式計算出的結果還需要輔以其他數據進行修正。[8][25]這個過程中會用到校準曲線(見下文),會將樣本中的14C含量轉化為樣本的曆法年齡。計算分幾步進行,當中會產生一個名為「放射性碳齡」(radiocarbon age)的值。放射性碳齡是指未經校準、假設大氣中14C/12C比值固定不變的前提下計算出來的樣本年代。其數值也不用普通的曆法時間來表示,而是用「放射性碳年」(radiocarbon year)為單位。[26][27] 計算放射性碳齡還要用到14C的半衰期。利比在1949年的論文中取的是5720±47年,該值由安托瓦內特·恩格米爾等人的研究得來。[28]這一數值與現代科學界使用的半衰期值頗為相近,只是在利比發表論文後不久,該值被修改為5568±30年,[29]並沿用了十餘載,又在1960年早期被改為5,730±40年,[30][31]導致大量此前發表的論文所得出的結論出錯,畢竟這裡所用的半衰期的殘留誤差達3%。[注 6]為了與這些早期文獻保持一致,1962年英國劍橋的放射性碳大會(Radiocarbon Conference)規定了一個新數值「利比半衰期」(Libby half-life),取5568年。現如今,人們在計算放射性碳齡時用的依然是利比半衰期,計算出的結果被稱為「慣用年齡」(Conventional Radiocarbon Age)。現代使用的14C大氣含量校準曲線——IntCal,也使用了慣用年齡,因此任何使用IntCal計算出來的數值都是校正過的準確時間。在學術論文中,習慣上會將未經校準的放射性碳年用雙引號括起來,以防讀者混淆——一來這個值計算時用的是錯誤的14C半衰期,二來該值未經大氣14C含量曲線進行校準。[26][27][33][注 7] 碳交換庫 大氣、生物圈、海洋中都含有碳元素,合稱為「碳交換庫」(carbon exchange reservoir)。[36]各個碳交換庫所貯的碳含量不同,與宇宙射線所產生的14C充分混合的時間也不一樣。這些因素會影響到各個碳庫中14C同12C的比例,因此不同碳庫中產出的樣本需要被區別對待。[8]大氣儲有占全體碳庫1.9%的碳元素。它是產生14C的地方,這些同位素只需要花不到七年的時間就能與其他碳元素充分混合。[37]大氣中14C對12C的比值被用作其他碳庫的基準值。如果其他碳庫的14C比12C值更低的話,要麼這些碳元素年代久遠導致14C已衰變,要麼這批碳元素並非來自大氣。[25]比方說,海洋表面的碳元素占了全體碳庫的2.4%,但其中14C的占比只有大氣的95%。[8]固然,大氣和洋面之間的碳交換隻需幾年光景,[38]但洋面自身又與深海海水反覆交融,其中後者的碳元素占了全體碳庫的90%有餘。[25]深海海水需要花1000年的時間才會回流至海洋表面,因此洋面的海水算是14C含量較低的「舊」海水和14C含量較高的「新」海水混合而來,同大氣中的碳元素呈動態平衡。[25] 活躍在海洋表面的生物,其體內的14C含量與其所居住的水層相近。由於海洋表面的14C/12C比值較低,海洋生物的放射性碳齡通常在400年左右。[39][40]相比之下,陸地上的生物和大氣之間的碳交換更為頻繁,因此其14C/12C的比值會與大氣的保持一致。[8][注 9]這些生物的碳元素占了碳庫的1.3%;全體海洋生物的總質量只有陸地生物的不到1%,因此圖表中並未列出。動植物屍體形成的有機物,其質量是現有生物圈的三倍有餘,由於它們不再與所處環境交換碳元素,其14C/12C比值比生物圈的要低。[8] 考量因素 各碳交換庫的14C/12C比值不盡相同。如果計算過程中只考慮樣本的14C含量,那麼計算結果常常不盡如人意。科學家通常會將以下額外四大類因素也納入考量範圍: 大氣變化 在放射性碳定年法(以下簡稱「碳定年法」)剛剛發明的一段時間裡,人們一直假設大氣中14C/12C比值維持了幾千年不變。為了驗證碳定年法的準確性,人們找來了幾樣年代已知的文物。起初,碳定年法得到的結果還和這些文物的實際年代差不多。可後來,在測算埃及已知最古老的王朝出土文物的年代時,碳定年法給出的結果和人們預估的古埃及年代之間開始出現偏差。在當時,人們還無從判斷碳定年法和預估埃及年代之間孰是孰非,但後來科學家意識到14C/12C比值並非此前所想的那般一成不變。在研究樹木年輪後,人們對這個比值的變動有了更深刻的了解。[42][43][44]人們在測算年輪的成分、年齡後,繪製出了長達8000年的年輪數據表。[42][注 10]1960年代,漢斯·修斯(英語:Hans Suess)利用樹木年輪計算得出,埃及學家預估的年份和碳定年法給出的結論實際上是一致的。一年生植物(如玉米)的14C/12C比值和其生長年份的大氣比值保持一致。而樹木則不同,每一年都會在外表長出一圈新年輪,新的14C並不會影響到樹幹裡層,反而是裡層的14C會逐漸衰變。因此,每一圈年輪都會記錄下其生長的那一年中大氣14C/12C的比值。透過這種方式,科學家整理出了碳定年法所需的大氣14C/12C比值:給定樹木樣本,已知樹木年齡、樣本中14C的原子數量N,人們可以套用衰變公式計算出年輪生長年份的14C原子數量N0,進而求得當年大氣的14C/12C比值。[42][44]利用這些數據,人們得出了碳定年法所需要的各年大氣14C/12C比值校準曲線(見下文)。[45] 19世紀,人們開始大量焚燒煤和燃油。這兩種化石燃料深埋於地下、年代久遠,它們的14C基本上都消耗光了。結果,它們焚燒產生的CO2大大降低了大氣中14C/12C的比值。若直接照搬碳定年法對20世紀早期的物品進行測定的話,結果會比實際年代要久遠得多。基於類似的原理,大城市附近的14C濃度也會低於大氣平均值。這一化石燃料效應,也被稱作「修斯效應」(Suess Effect,因漢斯·修斯在1955年首次報告這一問題),對大氣中14C產生了不小的影響。如果給予充分時間讓這些多出來的碳元素在各碳庫中充分交換的話,14C的活度只會減少0.2%。但由於深海海水需經多年才會與表層海水循環融合的緣故,14C的活度實際減少了3%。[42][46] 地上核試驗造成的影響更大,每次核試都會釋放大量中子並產生大批14C。從1950年開始,至1963年大氣核試驗被禁止這段時間內,據估算產生的14C有好幾噸。假若這批新14C立刻均勻分布至全體碳交換庫的話,大氣的14C/12C比值只會增長寥寥幾個百分點。但現實情況卻是大氣中的14C含量幾乎翻了一番,其中南、北半球分別在1966年、1964年達到峰值,被稱作「炸彈高峰(英語:bomb pulse)」。自那時起,碳元素逐漸交換環流至碳庫的其他部分,大氣14C含量也一直在下降。[42][46][47][41] 同位素分餾 光合作用是碳元素從大氣流入生物圈的主要方式。在光合作用時,12C比13C更好吸收,後者又比14C更容易吸收些。這三者的吸收率不同,導致大氣和植物的13C/12C和14C/12C的比值不盡相同,這一現象被稱為「同位素分餾」(isotopic fractionation)。[48][49] 要確定一株植物的分餾程度需要同時測量12C和13C兩個同位素的原子量,再將所得的13C/12C比值與基準線「PDB」[注 11]進行比較。之所以用13C/12C而不是14C/12C,是因為前者更容易測量,而且後者的比值也很容易推導出來:13C相對於12C的貧化現象與它們的原子質量之差成正比,因此14C的貧化是13C的兩倍。[25]13C的分餾,也稱作δ13C,是這樣計算的:[48] 其中「‰」代表計算結果用千分率表示。[48]由於PDB基準中的13C含量非常高[注 12],大部分測算的δ13C值為負數。 人們對海洋生物的光合作用細節了解的不夠深入,目前已知它們的δ13C值取決於水溫。溫度較高時,CO2不易溶於水,意味著參與光合作用的CO2更少,分餾作用也會減少。溫度高於14°C時,δ13C的值會更高。溫度較低時,CO2易溶於水,也就更容易為海洋生物獲取。[49]動物的δ13C值取決於它吃什麼,要是食用高δ13C的食物,其體內的δ13C也自然會更高。[48]動物自身的生物化學過程也會影響到結果。比如,骨質和骨膠原的13C含量通常會比該生物飲食的含量高(不過二者的成因不同)。骨骼中的這一13C富集現象也暗示了動物排泄物中的13C比它們吃進去的13C要少。[52] 鑑於13C通常會占樣本碳元素總量的1%,13C/12C的比值可透過質譜法準確量出。[25]目前,人們已透過實驗測量出了許多動植物的δ13C,但在使用碳定年法測算年代時最好不要援引這些數據,而應直接測量樣本的δ13C值。[48] 大氣CO2和海洋表面的碳酸鹽也會有同位素分餾的現象發生,大氣14C比12C更易溶於海洋之中。因此,海洋的14C/12C比值比大氣的要高1.5%。這一14C的濃縮現象與海底湧上來的「舊」海水(14C含量低)互相抵消,導致14C輻射的直接測量值與生物圈的其他地方大體一致。在將數據用同位素分餾校準後,人們測得海洋表面海水的表觀年齡約為400年。[25][40] 碳庫效應 在利比原先的假設中,全球的各個碳庫的14C/12C比值始終保持一致,[53]但後來人們陸陸續續發現了會改變碳庫比值的若干因素。[39] 大氣的CO2能溶於海洋表面的海水中形成碳酸根、碳酸氫根離子,從而將碳元素融進海洋中。同時,海水中的碳酸離子也會以CO2的形式重返大氣。[53]這一交換過程將大氣的14C帶到海洋表面,但要讓14C分散到整個水體還需要很長一段時間。深海海水和海洋表面的海水要花很久才會混合,而且就算如此各個海域的混合程度也參差不齊。深海海水主要透過上升流回到海洋表面,這一機制在赤道地區更常見些。此外,上升流也會受到海床和海岸線形狀,以及氣候、風場等因素的影響。總體看來,碳元素從大氣交換到洋面海水要比從洋面交換到深海中要快上許多,導致某些深海水體的海水的表觀放射性碳齡能有數千年。上升流將這些「舊」海水與洋面的「新」海水混合,導致人們測得洋面海水的表觀年齡為幾百年(經過同位素分餾校準)。[39]海洋碳庫效應並非均勻分布——平均表觀年齡是400年上下,但也有地理位置相近的水域的表觀年齡差距能達數百年。[39][40]這些差距可以用CALIB等軟體進行人工校準。[18]海洋碳庫效應也適用於各種海洋生物(如貝殼、鯨、海豹等),它們的放射性碳齡也通常有數百年。[39] 南、北半球的大氣環流各自相對獨立運作,因此兩個半球的空氣充分混合要花費不少時間。南半球的14C/12C比值比北半球的低,計算出的表觀年齡也比北半球的多40年左右。[注 13]這是由於南半球的海洋面積更大,導致大氣與海水之間的碳交換更為頻繁。受海洋效應的影響,海水中14C貧化得更嚴重些,導致南半球14C從大氣中流失的速度更快。[39][54]在南極附近,海水上升流更加強烈,也進一步加劇了南半球14C的流失。[15] 如果淡水中混有年代久遠碳元素(比如岩石中的碳)的話,水中的14C/12C比例會降低。比方說,石灰岩主要由碳酸鈣構成,流經石灰岩的河水會混入碳酸根離子。類似地,地下水也會攜有其流經岩石中的碳元素。這些岩石十分古老,其14C幾乎不含任何可檢測到的14C。任何經過這裡的水流的14C/12C比值都會下降,表觀年齡甚至會拔升至數千年,並影響到生長在水中的生物的檢測結果。[25]這一現象被稱作「硬水效應」,因為這些水中通常含有鈣離子,是硬水的特點。此外,腐殖質中的碳也能產生類似的影響,如果它們產生的時間比樣本的要晚的話,腐殖質可以反過來降低淡水樣本的表觀年齡。[39]硬水效應的影響不一,其偏差沒有統一的校準值。研究人員在面對這種情況時需要進行額外的操作來確定如何校準樣本測量結果,比如分析比較淡水的沉積包覆和其相關有機物的放射性碳齡。[55] 火山爆發時會噴射出大量的碳。這些碳元素原自地底,不含任何可檢測的14C,因此火山附近的14C/12C比值會下降。休眠火山也會噴發一些14C含量極低的物質。那些透過光合作用吸收這些碳元素的植物,其檢定的14C/12C比值就會更低些。比如,亞速爾富爾納斯(英語:Furnas)火山口附近的植物測得表觀年齡在250年—3320年之間。[56] 樣本污染 向樣本中添加任何含碳物質都會對樣本造成污染,導致測算結果不準確。樣本中混入表觀年齡低的「新」碳會導致碳定年法測算結果偏小,樣本年齡越大則偏差越嚴重。如果一個17,000年的樣本中混入了1%的「新」碳,其測算結果會減小600年;若是換成34,000年的樣本,同樣的樣本污染會造成4000年的偏差。反之,如果樣本中混入沒有任何14C殘留的「老」碳,會導致碳定年法測算結果偏大,其偏差值不受樣本年齡的影響。比方說,任何年代出土的樣本中如果混入了1%的「老」碳,會導致其碳定年法測算結果增大80年。[57]在選定、保存、測算非常古老的樣本時需要額外小心,因為樣本受污染物的干擾非常大。2014年,托馬斯·海厄姆(英語:Thomas Higham)等人表示,受「新碳」污染,許多文獻中有關尼安德塔人文物的日期過於新近。[58] 氣體正比計數器和液體閃爍計數儀都是在測量給定時間內樣本產生β粒子的數量。鑑於樣本質量已知,二者的測量結果都可以表示成「次數每分鐘每克碳」(記作cpm/g C),或者「貝克勒每千克碳」(記作Bq/kg C,此為國際單位制)。另外,這兩種測量方法都需要測量一個空白樣本的放射性活度。空白樣本是指「老」碳構成的樣本,這些碳元素年代久遠,不應帶有任何放射性。這樣一來科學家就能獲知背景輻射的強度,再將此值從先前樣本中測得的值減去,就能獲知該樣本自身的14C活度。此外,人們還會測定一個標準樣本的活度作為基準線。[73][注 14] AMS儀器可清點樣本中14C和12C的原子數量,從而直接得出14C/12C比值。樣本通常會被製成石墨以發射C-(帶一個負電荷的碳離子),並打入粒子加速器中。經過加速的碳離子會經過剝離器,失去若干電子變為陽離子(1—4個正電荷,即C+ — C4+)。隨後,取決於粒子加速器的結構,這些離子會經過磁場用以彎曲其行進路徑,較輕的離子比較重的離子的路徑偏折得更遠,因此碳離子會按其同位素種類分成一股股離子束。隨後,粒子探測器會統計14C離子束中離子的個數。不過,鑑於12C(和用於校正的13C)的離子束通量過大、來不及一個個探測,人們會用法拉第杯測量12C和13C離子束的電流大小。[76]剝離器會產生大量正電荷,能夠斷裂掉與14C質量相近的分子(如13CH)的化學鍵,從而排除雜質的干擾。[77]絕大多數AMS儀還能測量樣本的δ13C,用來計算樣本的放射性碳齡。[78]AMS相較於一般的質譜法,其優勢在於可以精準區分14N、13CH等質量極為接近的粒子。[62] 碳定年法的測定精度通常為平均值附近一個標準差(記作1σ)內。然而,1σ只有68%的置信水平,因此樣本的實際真實年代可能超出測量結果給定的年代範圍。1970年,大英博物館放射性碳實驗室(British Museum radiocarbon laboratory)進行了一項實驗,在6個月之內每周對同一個樣本測算一次年代。測算結果服從常態分布,但彼此間差異極大,有不少測量結果的1σ年代範圍互相之間不重合。比如有一個結果落在4250年—4390年,另一個落在4520年—4690年。[83] 未經校準的日期應當以這個格式列出:「<實驗室名>: <14C年> ± <區間> BP」。其中: 舉例來說,未經校準的日期「UtC-2020: 3510 ± 60 BP」表示樣本在烏得勒支·范德格拉夫實驗室(Utrecht van der Graaff Laboratorium)受檢,樣本編號2020,其中檢定年份是距今3510年(即公元前1560年),殘留誤差±60年。此格式有時會有一定的變化,比如「10 ka BP」指距今10,000放射性碳年(即公元前8050年),人們有時還會明確列出「14C yr BP」,以便與其他定年法(如熱釋光測年法)區分。[97] 1947年,科學家在死海附近的一個洞穴中發現了用希伯來語和亞拉姆語寫成的死海古卷,大部分可能是猶太小眾教派艾賽尼派所作。這些捲軸中包含了希伯來聖經已知的最早版本,因此對聖經文本的研究意義非凡。[109]這些捲軸被亞麻布包裹著。1955年,利比對裹著大以賽亞捲軸(英語:Great Isaiah scroll)的亞麻布取樣分析,估算年代為大約距今1,917±200年。[109][110]古文字學家根據書寫風格的分析估算了21個捲軸的年代。1990年代,人們從這21個捲軸中選了一大半進行取樣,再加上剩下沒有經過古文字學分析的捲軸,一同送往兩所AMS實驗室測定。年代結果分布在公元前4世紀早期到公元4世紀中期。送檢的捲軸中除了2個捲軸外,大多數捲軸測定的年代與古文字學分析的相差都不到100年。大以賽亞捲軸也在這批送檢樣本中,但由於對應時間段的校準曲線出現波動導致人們測算出兩個年代範圍:捲軸年代落在公元前355年至公元前295年的機率為15%,落在公元前210年至公元前45年的機率為84%,二者的置信水平均為2σ。但也有批評指出,在捲軸送檢之前,人們用現代生產的蓖麻油對這些捲軸進行過處理以方便閱讀,結果在用放射性碳定年法測算時沒能將這些蓖麻油清乾淨,導致樣本污染,測出的年代也過晚。支持和反對這一批評的論文都不少。[109] 放射性碳定年法還改變了人們對史前歐洲新發明傳播方式的看法。此前研究人員曾認為,新發明是透過陸路傳播逐漸滲透到各地的,或者是被侵略者帶入到被入侵的一方。但放射性碳定年法逐漸否定了這一看法,現在人們相信這些新發明是從當地社會內部自發地出現的。這一變革也被稱作「第二次放射性碳革命」。考古學家理察·艾金森(英語:Richard J.C. Atkinson)揶揄放射性碳定年法對史前英國研究的衝擊,稱其為給「逐漸惡化的入侵主義」的「放射……療法」。更廣泛地說,放射性碳定年法成功激起了考古學家對考古數據進行數理分析與統計的興趣。[113]泰勒也將AMS所帶來的衝擊、對小樣本的精準測定形容為第三次放射性碳革命的前奏。[114]